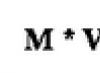Diferenciál funkcie v bode. Diferenciál funkcie jednej premennej

Ak funkcia v bode rozlíšiteľné , potom jeho prírastok môže byť vyjadrený ako súčet dvoch členov

. Tieto členy sú nekonečne malé funkcie at
.Prvý člen je lineárny vzhľadom na
,druhá je infinitesimálou vyššieho rádu ako
.naozaj,

Teda druhý termín na
má tendenciu rýchlejšie sa nulovať pri hľadaní prírastku funkcie
hlavnú úlohu hrá prvý termín
alebo (odkedy
)
.

Definícia . Hlavná časť prírastku funkcie
v bode , lineárne vzhľadom na
,nazývaný diferenciál funkcie v tomto bode a je určenýD Yalebodf(X)

. (2)

Môžeme teda dospieť k záveru: diferenciál nezávislej premennej sa zhoduje s jej prírastkom, tzn
.

Vzťah (2) teraz nadobúda formu

(3)

Komentujte . Vzorec (3) pre stručnosť sa často píše vo forme

(4)

Geometrický význam diferenciálu

Zvážte graf diferencovateľnej funkcie
. Body
a patria do grafu funkcie. Na mieste M nakreslená dotyčnica TO ku grafu funkcie, ktorej uhol je s kladným smerom osi
označovať podľa
. Nakreslíme rovné čiary MN rovnobežne s osou Vôl A
rovnobežne s osou Oj. Prírastok funkcie sa rovná dĺžke segmentu
. Z pravouhlého trojuholníka
, v ktorom
, dostaneme

Vyššie uvedené úvahy nám umožňujú dospieť k záveru:

Funkčný diferenciál
v bode je reprezentovaný prírastkom súradnice dotyčnice ku grafu tejto funkcie v jej zodpovedajúcom bode
.

Vzťah medzi diferenciálom a deriváciou

Zvážte vzorec (4)

Rozdeľme obe strany tejto rovnosti podľa dx, Potom

teda derivácia funkcie sa rovná pomeru jej diferenciálu k diferenciálu nezávislej premennej.

Často tento postoj zaobchádzať jednoducho ako so symbolom označujúcim deriváciu funkcie pri argumentom X.

Vhodné zápisy pre derivát sú tiež:

,
a tak ďalej.

Používajú sa aj záznamy

,
,

obzvlášť výhodné pri použití derivátu komplexného výrazu.

2. Diferenciál súčtu, súčinu a kvocientu.

Keďže diferenciál sa získa z derivácie vynásobením diferenciálom nezávislej premennej, potom, keď poznáme derivácie základných elementárnych funkcií, ako aj pravidlá pre hľadanie derivácií, možno dospieť k podobným pravidlám hľadania diferenciálov.

1 0 . Rozdiel konštanty je nula

2 0 . Diferenciál algebraického súčtu konečného počtu diferencovateľných funkcií sa rovná algebraickému súčtu diferenciálov týchto funkcií

3 0 . Diferenciál súčinu dvoch diferencovateľných funkcií sa rovná súčtu súčinov prvej funkcie diferenciálom druhej a druhej funkcie diferenciálom prvej funkcie

Dôsledok. Konštantný multiplikátor je možné vyňať z diferenciálneho znamienka

Príklad. Nájdite diferenciál funkcie.

Riešenie: Napíšme túto funkciu do formulára

potom dostaneme

4. Funkcie definované parametricky, ich diferenciácia.

Definícia . Funkcia
sa hovorí, že je daný parametricky, ak obe premenné X A pri každá je definovaná samostatne ako jednohodnotové funkcie tej istej pomocnej premennej - parametrat:

Kdetsa mení v rámci
.

Komentujte . Parametrická špecifikácia funkcií je široko používaná v teoretickej mechanike, kde je parameter t označuje čas a rovnice
predstavujú zákony zmeny v projekciách pohybujúceho sa bodu
na osi
A
.

Komentujte . Uveďme si parametrické rovnice kružnice a elipsy.

a) Kružnica so stredom v počiatku a polomerom r má parametrické rovnice:

Kde
.

b) Napíšme parametrické rovnice pre elipsu:

Kde
.

Vylúčením parametra t Z parametrických rovníc uvažovaných čiar možno dospieť k ich kanonickým rovniciam.

Veta . Ak funkcia y z argumentu x je dané parametricky rovnicami
, Kde
A
diferencovateľné vzhľadom natfunkcie a
, To

Príklad. Nájdite deriváciu funkcie pri od X, dané parametrickými rovnicami.

Riešenie.
.

Ak funkcia v bode rozlíšiteľné , potom jeho prírastok môže byť vyjadrený ako súčet dvoch členov

. Tieto členy sú nekonečne malé funkcie at
.Prvý člen je lineárny vzhľadom na
,druhá je infinitesimálou vyššieho rádu ako
.naozaj,

Teda druhý termín na
má tendenciu rýchlejšie sa nulovať pri hľadaní prírastku funkcie
hlavnú úlohu hrá prvý termín
alebo (odkedy
)
.

Definícia . Hlavná časť prírastku funkcie
v bode , lineárne vzhľadom na
,nazývaný diferenciál funkcie v tomto bode a je určenýD Yalebodf(X)

. (2)

Môžeme teda dospieť k záveru: diferenciál nezávislej premennej sa zhoduje s jej prírastkom, tzn
.

Vzťah (2) teraz nadobúda formu

(3)

Komentujte . Vzorec (3) pre stručnosť sa často píše vo forme

(4)

Geometrický význam diferenciálu

Vyššie uvedené úvahy nám umožňujú dospieť k záveru:

Funkčný diferenciál
v bode je reprezentovaný prírastkom súradnice dotyčnice ku grafu tejto funkcie v jej zodpovedajúcom bode
.

Vzťah medzi diferenciálom a deriváciou

Zvážte vzorec (4)

Rozdeľme obe strany tejto rovnosti podľa dx, Potom

teda derivácia funkcie sa rovná pomeru jej diferenciálu k diferenciálu nezávislej premennej.

Často tento postoj zaobchádzať jednoducho ako so symbolom označujúcim deriváciu funkcie pri argumentom X.

Vhodné zápisy pre derivát sú tiež:

,
a tak ďalej.

Používajú sa aj záznamy

,
,

obzvlášť výhodné pri použití derivátu komplexného výrazu.

2. Diferenciál súčtu, súčinu a kvocientu.

1 0 . Rozdiel konštanty je nula

2 0 . Diferenciál algebraického súčtu konečného počtu diferencovateľných funkcií sa rovná algebraickému súčtu diferenciálov týchto funkcií

3 0 . Diferenciál súčinu dvoch diferencovateľných funkcií sa rovná súčtu súčinov prvej funkcie diferenciálom druhej a druhej funkcie diferenciálom prvej funkcie

Dôsledok. Konštantný multiplikátor je možné vyňať z diferenciálneho znamienka

Príklad. Nájdite diferenciál funkcie.

Riešenie: Napíšme túto funkciu do formulára

potom dostaneme

4. Funkcie definované parametricky, ich diferenciácia.

Definícia . Funkcia
sa hovorí, že je daný parametricky, ak obe premenné X A pri každá je definovaná samostatne ako jednohodnotové funkcie tej istej pomocnej premennej - parametrat:

Kdetsa mení v rámci
.

Komentujte . Uveďme si parametrické rovnice kružnice a elipsy.

a) Kružnica so stredom v počiatku a polomerom r má parametrické rovnice:

Kde
.

b) Napíšme parametrické rovnice pre elipsu:

Kde
.

Vylúčením parametra t Z parametrických rovníc uvažovaných čiar možno dospieť k ich kanonickým rovniciam.

Veta . Ak funkcia y z argumentu x je dané parametricky rovnicami
, Kde
A
diferencovateľné vzhľadom natfunkcie a
, To

Príklad. Nájdite deriváciu funkcie pri od X, dané parametrickými rovnicami.

Riešenie.
.

Pojem a geometrický význam diferenciálu

Definícia. Diferenciál funkcie v určitom bode x je hlavnou, lineárnou časťou prírastku funkcie.

Diferenciál funkcie y = f(x) sa rovná súčinu jej derivácie a prírastku nezávisle premennej x (argument).

Píše sa to takto:

Geometrický význam diferenciálu. Diferenciál funkcie y = f(x) sa rovná prírastku v ordináte tečny S nakreslenej ku grafu tejto funkcie v bode M(x; y), keď sa x (argument) zmení o hodnotu (pozri obrázok).

Prečo je možné použiť diferenciál v približných výpočtoch?

Diferenciál je hlavná, relatívne lineárna časť prírastku funkcie; čím menší, tým väčší podiel prírastku tvorí táto časť. Môžete si to overiť mentálnym posunutím kolmice spustenej z bodu P (pozri obrázok) k osi Ox, bližšie k začiatku. Preto pre malé hodnoty (a pre ) možno prírastok funkcie približne nahradiť jej hlavnou časťou, t.j.

O rôznych formách písania diferenciálu

Diferenciál funkcie v bode x označíme

teda

, (2)

keďže diferenciál funkcie y = f(x) sa rovná súčinu jej derivácie a prírastku nezávislej premennej.

Komentujte. Je potrebné mať na pamäti, že ak x je počiatočná hodnota argumentu a je to inkrementovaná hodnota, potom derivácia v diferenciálnom výraze sa berie v počiatočnom bode x; vo vzorci (1) to zo záznamu nie je viditeľné.

Diferenciál funkcie možno zapísať v inej forme:

(4)

Diferenciálne vlastnosti

V tomto a nasledujúcich odsekoch budeme považovať každú z funkcií za diferencovateľnú pre všetky uvažované hodnoty jej argumentov.

Diferenciál má vlastnosti podobné vlastnostiam derivátu:

(C je konštantná hodnota) (5)

(6)

(7)

(9)

Vzorce (5) – (9) sa získajú zo zodpovedajúcich vzorcov pre deriváciu vynásobením oboch strán každej rovnosti číslom .

Aplikácia diferenciálu v približných výpočtoch

Približná rovnosť stanovená v druhom odseku

umožňuje použiť diferenciál na približné výpočty funkčných hodnôt.

Zapíšme si približnú rovnosť podrobnejšie. Pretože

Absolútne a relatívne chyby približných výpočtov

Pomocou približnej hodnoty čísla musíte vedieť posúdiť stupeň jeho presnosti. Na tento účel sa vypočítajú jeho absolútne a relatívne chyby.

Absolútna chyba približného čísla sa rovná absolútnej hodnote rozdielu medzi presným číslom a jeho približnou hodnotou:

Relatívna chyba približného čísla je pomer absolútnej chyby tohto čísla k absolútnej hodnote zodpovedajúceho presného čísla:

Ak presné číslo nie je známe, potom

Niekedy je pred použitím vzorca (11) potrebné najprv transformovať pôvodnú hodnotu. Zvyčajne sa to robí na dva účely. Po prvé, je potrebné zabezpečiť, aby hodnota bola dostatočne malá v porovnaní s , pretože čím menšia , tým presnejší je výsledok približného výpočtu. Po druhé, je žiaduce, aby sa hodnota vypočítala jednoducho.

24. Aplikácia funkčného diferenciálu na približné výpočty

Použitie diferenciálu na približné výpočty

Koncept diferenciálu naznačuje, že ak je akýkoľvek proces svojou povahou zmeny blízky lineárnemu, potom sa prírastok funkcie len málo líši od diferenciálu. Okrem toho, ak má funkcia v určitom bode x konečnú deriváciu, potom jej prírastok a diferenciál sú tiež nekonečne malé ako , majú tendenciu k nule:

Keďže diferencovaná funkcia je spojitá,

Pretože súčin obmedzenej funkcie a infinitezimálnej funkcie, pretože DX má tendenciu k nule, je nekonečne malá funkcia.

Okrem toho sú tieto dve infinitezimálne funkcie ekvivalentné:

Ekvivalencia umožňuje, s malými prírastkami argumentu, približne vypočítať

Čo môže tento vzorec poskytnúť? Nechajte hodnoty a vypočítajte relatívne jednoducho v určitom bode. Potom v inom bode, neďaleko , je možné nasledujúce zobrazenie:

Tu zostáva otvorená otázka o presnosti získaného výsledku. Táto okolnosť znižuje hodnotu tohto približného výpočtového vzorca, ale je všeobecne užitočný a v praxi široko používaný.

Pozrime sa na príklad. Aká bude prepona tohto trojuholníka v pravouhlom trojuholníku, ak sa rameno a zmenší o 0,2 m (obr. 11.5, a)?

Nájdite pôvodnú dĺžku prepony:

Po zmenšení ramena a o 0,2 m bude prepona rovná (obr. 11.5, a)

Aplikujme teraz vzorec (11.16), aby sme približne našli c v súvislosti s poklesom v ramene a, berúc do úvahy funkciu tvaru:

(B = Konšt.);

V oboch prípadoch sme dostali približnú hodnotu požadovanej hodnoty. Ale v prvom prípade chyba vzniká ako výsledok približných výpočtov a v druhom, pomerne jednoduchšom prípade, kvôli použitiu približného vzorca (môže sa k nemu pridať aj chyba spôsobená približnými výpočtami). Všimnite si, že keď sa rameno a zníži o 0,2 m, prepona c sa zníži približne o 0,08 m a približné hodnoty, ktoré sme získali, sa líšia iba o 0,001 m.

Uvažujme o inej situácii: v tom istom trojuholníku znížime preponu c o 0,2 m, pričom rameno b zostane nezmenené (obr. 11.5, b). Poďme určiť, ako sa v tomto prípade zmení časť A:

25. Aplikácia derivácie na štúdium funkcií a vykresľovanie grafov

Ak je na určitom intervale grafom funkcie súvislá čiara, inými slovami čiara, ktorú možno nakresliť z listu papiera bez ceruzky, potom sa takáto funkcia na tomto intervale nazýva spojitá. Existujú aj funkcie, ktoré nie sú spojité. Ako príklad uvažujme graf funkcie, ktorá na intervaloch a [s; b] je spojitý, ale v bode
x = c je nespojité, a preto nie je spojité cez celý segment. Všetky funkcie, ktoré študujeme v kurze školskej matematiky, sú spojité funkcie na každom intervale, na ktorom sú definované.

Všimnite si, že ak má funkcia deriváciu na určitom intervale, potom je na tomto intervale spojitá.

Opačné tvrdenie je nesprávne. Funkcia, ktorá je spojitá na intervale, nemusí mať v niektorých bodoch tohto intervalu deriváciu. Napríklad funkcia
y = |log 2 x| spojitá na intervale x > 0, ale v bode x = 1 nemá deriváciu, pretože v tomto bode graf funkcie dotyčnice nemá dotyčnicu.

Pozrime sa na vykresľovanie grafov pomocou derivácie.

Nakreslite graf funkcie f(x) = x 3 – 2x 2 + x.

1) Táto funkcia je definovaná pre všetky x € R.

2) Nájdite intervaly monotónnosti uvažovanej funkcie a jej extrémne body pomocou derivácie. Derivácia sa rovná f "(x) = 3x 2 – 4x + 1. Nájdite stacionárne body:
3x 2 – 4x + 1 = 0, odkiaľ x 1 = 1/3, x 2 = 1.

Na určenie znamienka derivácie rozkladáme kvadratické trinómy 3x 2 – 4x + 1:
f "(x) = 3(x – 1/3)(x – 1). Preto na intervaloch x< 1/3 и х >1 derivát je kladný; To znamená, že funkcia sa v týchto intervaloch zvyšuje.

Derivát je negatívny na 1/3< х < 1; следовательно, функция убывает на этом интервале.

Bod x 1 = 1/3 je maximálny bod, pretože napravo od tohto bodu funkcia klesá a vľavo rastie. V tomto bode je hodnota funkcie f (1/3) = (1/3) 3 – 2(1/3) 2 + 1/3 = 4/27.

Minimálny bod je bod x2 = 1, keďže vľavo od tohto bodu funkcia klesá a vpravo rastie; jeho hodnota v tomto minimálnom bode je f (1) = 0.

3) Pri konštrukcii grafu sa zvyčajne nachádzajú priesečníky grafu so súradnicovými osami. Pretože f(0) = 0, graf prechádza počiatkom. Vyriešením rovnice f(0) = 0 nájdeme priesečníky grafu s osou x:

x 3 – 2x 2 + x = 0, x(x 2 – 2x + 1) = 0, x(x – 1) 2 = 0, odkiaľ x = 0, x = 1.

4) Pre presnejšie vykreslenie nájdime funkčné hodnoty v ďalších dvoch bodoch: f(-1/2) = -9/8, f(2) = 2.

5) Pomocou výsledkov štúdie (body 1 – 4) zostavíme graf funkcie y = x 3 – 2x 2 + x.

Na zostavenie grafu funkcie sa zvyčajne najprv skúmajú vlastnosti tejto funkcie pomocou jej derivácie podľa schémy podobnej schéme riešenia úlohy 1.

Preto pri skúmaní vlastností funkcie musíte nájsť:

1) rozsah jeho definície;

2) derivát;

3) stacionárne body;

4) intervaly nárastu a poklesu;

5) extrémne body a funkčné hodnoty v týchto bodoch.

Výsledky výskumu je vhodné zaznamenávať vo forme tabuľky. Potom sa pomocou tabuľky vykreslí graf funkcie. Pre presnejšie zostrojenie grafu sa zvyčajne nájdu body jeho priesečníka so súradnicovými osami a v prípade potreby aj niekoľko ďalších bodov grafu.

Ak stojíme pred párnou alebo nepárnou funkciou, potom na zostrojenie jej grafu stačí naštudovať si vlastnosti a zostrojiť jej graf pre x > 0 a potom ho symetricky odraziť podľa ordinátnej osi (počiatku). Napríklad pri analýze funkcie f(x) = x + 4/x dospejeme k záveru, že táto funkcia je nepárna: f(-x) = -x + 4/(-x) = -(x + 4/ x) = -f(x). Po dokončení všetkých bodov plánu zostavíme graf funkcie pre x > 0 a graf tejto funkcie pre x< 0 получаем посредством симметричного отражения графика при х >0 vzhľadom na pôvod.

Pre stručnosť, riešenie problémov pri zostavovaní grafov funkcií sa väčšina úvah uskutočňuje ústne.

Poznamenávame tiež, že pri riešení niektorých problémov sa môžeme stretnúť s potrebou študovať funkciu nie v celom definičnom obore, ale iba v určitom intervale, napríklad ak potrebujeme vykresliť povedzme funkciu f(x). ) = 1 + 2x 2 – x 4 na segmente [-1; 2].

26. Primitívna derivácia funkcie. Neurčitý integrál a jeho vlastnosti

Definícia primitívneho derivátu.

Primitívna derivácia funkcie f(x) na intervale (a; b) je taká funkcia F(x), že rovnosť platí pre ľubovoľné x z daného intervalu.

Ak vezmeme do úvahy skutočnosť, že derivácia konštanty C sa rovná nule, potom platí rovnosť . Funkcia f(x) má teda množinu primitív F(x)+C pre ľubovoľnú konštantu C a tieto primitívy sa od seba líšia ľubovoľnou konštantnou hodnotou.

Definícia neurčitého integrálu.

Celá množina primitívnych derivátov funkcie f(x) sa nazýva neurčitý integrál tejto funkcie a označuje sa .

Výraz sa nazýva integrand a f(x) sa nazýva integrand. Integrand predstavuje diferenciál funkcie f(x).

Akcia hľadania neznámej funkcie danej jej diferenciálom sa nazýva neurčitá integrácia, pretože výsledkom integrácie nie je jedna funkcia F(x), ale množina jej primitívnych funkcií F(x)+C.

Na základe vlastností derivácie je možné formulovať a dokázať vlastnosti neurčitého integrálu (vlastnosti primitívnej derivácie).

1.
Derivácia výsledku integrácie sa rovná integrandu.

2.
Neurčitý integrál diferenciálu funkcie sa rovná súčtu samotnej funkcie a ľubovoľnej konštanty.

3. , kde k je ľubovoľná konštanta.
Koeficient možno vyňať ako znamienko neurčitého integrálu.

4.
Neurčitý integrál súčtu/rozdielu funkcií sa rovná súčtu/rozdielu neurčitých integrálov funkcií.

Pre objasnenie sú uvedené medziľahlé rovnosti prvej a druhej vlastnosti neurčitého integrálu.

Na dôkaz tretej a štvrtej vlastnosti stačí nájsť deriváty pravých strán rovnosti:

Tieto derivácie sa rovnajú integrandom, čo je dôkazom prvej vlastnosti. Používa sa aj pri posledných prechodoch.

Problém integrácie je teda opakom problému diferenciácie a medzi týmito problémami je veľmi úzka súvislosť:

· prvá vlastnosť umožňuje kontrolu integrácie. Na kontrolu správnosti vykonanej integrácie stačí vypočítať deriváciu získaného výsledku. Ak sa funkcia získaná ako výsledok diferenciácie ukáže ako rovná integrandu, znamená to, že integrácia bola vykonaná správne;

· druhá vlastnosť neurčitého integrálu umožňuje nájsť jeho primitívnu vlastnosť pomocou známeho diferenciálu funkcie. Na tejto vlastnosti je založený priamy výpočet neurčitých integrálov.

Pozrime sa na príklad.

Nájdite primitívnu vlastnosť funkcie, ktorej hodnota sa rovná jednej v x = 1.

Vieme to z diferenciálneho počtu (stačí si pozrieť tabuľku derivácií základných elementárnych funkcií). teda . Pri druhej nehnuteľnosti . To znamená, že máme veľa primitívnych derivátov. Pre x = 1 dostaneme hodnotu . Podľa podmienky sa táto hodnota musí rovnať jednej, teda C = 1. Požadovaná primitívna derivácia bude mať tvar .

Ak sa tabuľka derivácií základných elementárnych funkcií prepíše do tvaru diferenciálov, potom z nej pomocou druhej vlastnosti neurčitého integrálu možno zostaviť tabuľku primitív.

Súvisiace informácie.

Ako vidíte, na nájdenie diferenciálu musíte deriváciu vynásobiť dx. To vám umožní okamžite zapísať zodpovedajúcu tabuľku pre diferenciály z tabuľky vzorcov pre deriváty.

Celkový diferenciál pre funkciu dvoch premenných:

Celkový diferenciál pre funkciu troch premenných sa rovná súčtu parciálnych diferenciálov: d f(x,y,z)=d x f(x,y,z)dx+d y f(x,y,z)dy+d z f(x ,y,z)dz

Definícia . Funkcia y=f(x) sa nazýva diferencovateľná v bode x 0, ak jej prírastok v tomto bode možno znázorniť ako ∆y=A∆x + α(∆x)∆x, kde A je konštanta a α(∆ x) – nekonečne malé ako ∆x → 0.
Požiadavka, aby bola funkcia diferencovateľná v bode, je ekvivalentná existencii derivácie v tomto bode a A = f'(x 0).

Nech f(x) je diferencovateľné v bode x 0 a f "(x 0)≠0, potom ∆y=f'(x 0)∆x + α∆x, kde α= α(∆x) →0 v ∆x →0 Veličina ∆y a každý člen na pravej strane sú nekonečne malé veličiny pre ∆x→0. , to znamená, že α(∆x)∆x je infinitezimálom vyššieho rádu ako f’(x 0)∆x.
, teda ∆y~f’(x 0)∆x. V dôsledku toho f’(x 0)∆x predstavuje hlavnú a zároveň lineárnu časť ∆x prírastku ∆y (lineárnu, čo znamená, že obsahuje ∆x k prvej mocnine). Tento člen sa nazýva diferenciál funkcie y=f(x) v bode x 0 a označuje sa dy(x 0) alebo df(x 0). Takže pre ľubovoľné hodnoty x
dy=f′(x)∆x. (1)
Potom nastavte dx=∆x
dy=f'(x)dx. (2)

Príklad. Nájdite derivácie a diferenciály týchto funkcií.
a) y = 4 tan2 x
Riešenie:

rozdiel:
b)
Riešenie:

rozdiel:
c) y=arcsin 2 (lnx)
Riešenie:

rozdiel:
G)
Riešenie:
=
rozdiel:

Príklad. Pre funkciu y=x 3 nájdite výraz pre ∆y a dy pre niektoré hodnoty x a ∆x.
Riešenie. ∆y = (x+∆x) 3 – x 3 = x 3 + 3x 2 ∆x +3x∆x 2 + ∆x 3 – x 3 = 3x 2 ∆x+3x∆x 2 +∆x 3 ; dy=3x 2 ∆x (vzali sme hlavnú lineárnu časť ∆y vo vzťahu k ∆x). V tomto prípade α(∆x)∆x = 3x∆x 2 + ∆x 3.

Keďže sú neoddeliteľne spojené, obe sa už niekoľko storočí aktívne používajú pri riešení takmer všetkých problémov, ktoré vznikli v procese ľudskej vedeckej a technickej činnosti.

Vznik pojmu diferenciál

Slávny nemecký matematik Gottfried Wilhelm Leibniz, jeden z tvorcov (spolu s Isaacom Newtonom) diferenciálneho počtu, ako prvý vysvetlil, čo je diferenciál. Predtým matematici 17. stor. bola použitá veľmi nejasná a vágna predstava o nejakej infinitezimálnej „nedeliteľnej“ časti ktorejkoľvek známej funkcie, ktorá predstavovala veľmi malú konštantnú hodnotu, ktorá sa však nerovnala nule, teda menšia ako hodnota funkcie jednoducho nemôže byť. Odtiaľto bol už len jeden krok k zavedeniu konceptu nekonečne malých prírastkov argumentov funkcií a zodpovedajúcich prírastkov samotných funkcií, vyjadrených ich derivátmi. A tento krok urobili takmer súčasne aj dvaja vyššie spomínaní veľkí vedci.

Na základe potreby riešiť naliehavé praktické problémy mechaniky, ktoré pred vedu postavil rýchlo sa rozvíjajúci priemysel a technika, vytvorili Newton a Leibniz všeobecné metódy na zistenie rýchlosti zmeny funkcií (predovšetkým vo vzťahu k mechanickej rýchlosti telesa pozdĺž známej trajektórie), čo viedlo k zavedeniu takých konceptov, ako je derivácia a diferenciál funkcie, a tiež našiel algoritmus na riešenie inverzného problému, ako nájsť prejdenú vzdialenosť pomocou známej (premennej) rýchlosti, čo viedlo k vzniku pojmu integrál.

V prácach Leibniza a Newtona sa prvýkrát objavila myšlienka, že diferenciály sú hlavnými časťami prírastkov funkcií Δy úmerných prírastkom argumentov Δx, ktoré možno úspešne použiť na výpočet ich hodnôt. Inými slovami, zistili, že prírastok funkcie môže byť v ktoromkoľvek bode (v rámci domény jej definície) vyjadrený prostredníctvom jej derivácie ako Δу = y"(x) Δх + αΔх, kde α Δх je zvyšok smerujúci k nula ako Δх→ 0, oveľa rýchlejšie ako samotná Δx.

Podľa zakladateľov matematickej analýzy sú diferenciály presne prvými pojmami vo výrazoch pre prírastky akýchkoľvek funkcií. Keďže ešte nemali jasne formulovaný koncept limity postupností, intuitívne pochopili, že hodnota diferenciálu smeruje k derivácii funkcie ako Δх→0 - Δу/Δх→ y"(x).

Na rozdiel od Newtona, ktorý bol v prvom rade fyzik a považoval matematický aparát za pomocný nástroj na štúdium fyzikálnych problémov, Leibniz venoval väčšiu pozornosť tejto sade nástrojov, vrátane systému vizuálnych a zrozumiteľných zápisov matematických veličín. Bol to on, kto navrhol všeobecne uznávaný zápis pre diferenciály funkcie dy = y"(x)dx, argument dx a deriváciu funkcie v tvare ich pomeru y"(x) = dy/dx.

Moderná definícia

Čo je to diferenciál z pohľadu modernej matematiky? Úzko súvisí s pojmom prírastok premennej. Ak premenná y najprv nadobudne hodnotu y = y 1 a potom y = y 2, potom sa rozdiel y 2 ─ y 1 nazýva prírastok y.

Prírastok môže byť kladný. záporné a rovné nule. Slovo „prírastok“ označujeme Δ, zápis Δу (čítaj „delta y“) označuje prírastok hodnoty y. takže Δу = y 2 ─ y 1 .

Ak hodnotu Δу ľubovoľnej funkcie y = f (x) môžeme znázorniť v tvare Δу = A Δх + α, kde A nezávisí od Δх, t.j. A = konšt. pre dané x a člen α pre Δх →0 má tendenciu byť ešte rýchlejší ako samotný Δx, potom prvý („hlavný“) člen, úmerný Δx, je pre y = f (x) diferenciál, označovaný dy alebo df(x) (čítaj „de igrek“ , „de ef z x“). Preto sú diferenciály „hlavnými“ zložkami prírastkov funkcií, ktoré sú lineárne vzhľadom na Δx.

Mechanický výklad

Nech s = f (t) je vzdialenosť priamočiaro idúceho vozidla od počiatočnej polohy (t je čas jazdy). Prírastok Δs je dráha bodu počas časového intervalu Δt a diferenciál ds = f" (t) Δt je dráha, ktorú by bod prešiel za rovnaký čas Δt, keby si zachoval rýchlosť f"(t ) dosiahnuté časom t . Pre infinitezimálne Δt sa imaginárna dráha ds líši od skutočnej Δs o nekonečne malé množstvo, ktoré má vyšší rád vzhľadom na Δt. Ak rýchlosť v okamihu t nie je nulová, potom ds udáva približnú hodnotu malého posunutia bodu.

Geometrická interpretácia

Nech čiara L je graf y = f(x). Potom Δ x = MQ, Δу = QM" (pozri obrázok nižšie). Dotyčnica MN rozdeľuje segment Δy na dve časti, QN a NM." Prvý je úmerný Δх a rovná sa QN = MQ∙tg (uhol QMN) = Δх f "(x), t.j. QN je diferenciál dy.

Druhá časť NM" udáva rozdiel Δу ─ dy, s Δх→0 sa dĺžka NM" zmenšuje ešte rýchlejšie ako prírastok argumentu, t.j. jeho rádovo maličkosti je vyššie ako Δх. V uvažovanom prípade pre f "(x) ≠ 0 (tangens nie je rovnobežná s OX) sú segmenty QM" a QN ekvivalentné; inými slovami, NM" klesá rýchlejšie (jeho rádovo menšie je vyššie) ako celkový prírastok Δу = QM". To je možné vidieť na obrázku (keďže sa M "približuje k M, segment NM" tvorí stále menšie percento segmentu QM").

Takže graficky sa diferenciál ľubovoľnej funkcie rovná prírastku ordináty jej dotyčnice.

Derivát a diferenciál

Koeficient A v prvom člene výrazu pre prírastok funkcie sa rovná hodnote jej derivácie f "(x). Platí teda vzťah - dy = f "(x)Δx, alebo df (x) = f "(x)Δx.

Je známe, že prírastok nezávislého argumentu sa rovná jeho diferenciálu Δх = dx. Podľa toho môžeme napísať: f "(x) dx = dy.

Hľadanie (niekedy nazývané „riešenie“) diferenciálov sa riadi rovnakými pravidlami ako pre deriváty. Ich zoznam je uvedený nižšie.

Čo je univerzálnejšie: prírastok argumentu alebo jeho diferenciál

Tu je potrebné urobiť niekoľko objasnení. Znázornenie diferenciálu hodnotou f "(x)Δx je možné, keď sa x považuje za argument. Funkcia však môže byť zložitá, v ktorej x môže byť funkciou nejakého argumentu t. Potom diferenciál predstavujeme výrazom f " (x)Δx je spravidla nemožné; okrem prípadu lineárnej závislosti x = pri + b.

Čo sa týka vzorca f "(x)dx = dy, tak v prípade nezávislého argumentu x (potom dx = Δx) aj v prípade parametrickej závislosti x na t predstavuje diferenciál.

Napríklad výraz 2 x Δx predstavuje pre y = x 2 jeho diferenciál, keď x je argument. Položme teraz x = t 2 a uvažujme t ako argument. Potom y = x 2 = t 4.

Tento výraz nie je úmerný Δt, a preto teraz 2xΔx nie je diferenciál. Dá sa zistiť z rovnice y = x 2 = t 4. Ukázalo sa, že sa rovná dy=4t 3 Δt.

Ak vezmeme výraz 2xdx, potom predstavuje diferenciál y = x 2 pre ľubovoľný argument t. V skutočnosti pre x = t 2 dostaneme dx = 2tΔt.

To znamená, že 2xdx = 2t 2 2tΔt = 4t 3 Δt, t.j. diferenciálne výrazy zapísané v termínoch dvoch rôznych premenných sa zhodovali.

Nahradenie prírastkov diferenciálmi

Ak f "(x) ≠ 0, potom Δу a dy sú ekvivalentné (pre Δх→0); ak f "(x) = 0 (čo znamená dy = 0), nie sú ekvivalentné.

Napríklad, ak y = x 2, potom Δу = (x + Δх) 2 ─ x 2 = 2xΔх + Δх 2 a dy = 2xΔх. Ak x=3, potom máme Δу = 6Δх + Δх 2 a dy = 6Δх, ktoré sú ekvivalentné vďaka Δх 2 →0, pri x=0 hodnoty Δу = Δх 2 a dy=0 nie sú ekvivalentné.

Táto skutočnosť spolu s jednoduchou štruktúrou diferenciálu (t. j. linearita vzhľadom na Δx) sa často používa pri približných výpočtoch za predpokladu, že Δy ≈ dy pre malé Δx. Nájdenie diferenciálu funkcie je zvyčajne jednoduchšie ako výpočet presnej hodnoty prírastku.

Napríklad máme kovovú kocku s hranou x = 10,00 cm Pri zahriatí sa hrana predĺžila o Δx = 0,001 cm. Máme V = x 2, teda dV = 3x 2 Δx = 3∙10 2 ∙0/01 = 3 (cm 3). Zvýšenie objemu ΔV je ekvivalentné diferenciálnemu dV, takže ΔV = 3 cm 3 . Úplný výpočet by dal ΔV = 10,01 3 ─ 10 3 = 3,003001. Ale v tomto výsledku sú všetky čísla okrem prvého nespoľahlivé; to znamená, že na tom nezáleží, musíte to zaokrúhliť na 3 cm 3.

Je zrejmé, že tento prístup je užitočný iba vtedy, ak je možné odhadnúť veľkosť chyby, ktorú spôsobuje.

Funkčný diferenciál: príklady

Skúsme nájsť diferenciál funkcie y = x 3 bez nájdenia derivácie. Dajme argumentu prírastok a definujme Δу.

Δу = (Δх + x) 3 ─ x 3 = 3x 2 Δх + (3xΔх 2 + Δх 3).

Tu koeficient A = 3x 2 nezávisí od Δx, takže prvý člen je úmerný Δx, zatiaľ čo druhý člen 3xΔx 2 + Δx 3 pri Δx→0 klesá rýchlejšie ako prírastok argumentu. Preto výraz 3x 2 Δx je diferenciál y = x 3:

dy=3x 2 Δх=3x 2 dx alebo d(x 3) = 3x 2 dx.

V tomto prípade d(x 3) / dx = 3x 2.

Nájdime teraz dy funkcie y = 1/x prostredníctvom jej derivácie. Potom d(1/x) / dx = ─1/x 2. Preto dy = ─ Δx/x 2.

Diferenciály základných algebraických funkcií sú uvedené nižšie.

Približné výpočty pomocou diferenciálu

Často nie je ťažké vypočítať funkciu f (x), ako aj jej deriváciu f "(x) v x=a, ale urobiť to isté v blízkosti bodu x=a nie je jednoduché. Potom približný výraz prichádza na pomoc

f(a + Δх) ≈ f "(a)Δх + f(a).

Udáva približnú hodnotu funkcie pre malé prírastky Δх cez jej diferenciál f "(a)Δх.

V dôsledku toho tento vzorec poskytuje približný výraz pre funkciu na konci určitého úseku dĺžky Δx vo forme súčtu jeho hodnoty v počiatočnom bode tohto úseku (x=a) a diferenciálu na rovnakom začiatku. bod. Chyba v tejto metóde určenia hodnoty funkcie je znázornená na obrázku nižšie.

Známy je však aj presný výraz pre hodnotu funkcie pre x=a+Δх daný vzorcom konečného prírastku (alebo inými slovami Lagrangeovým vzorcom)

f(a+ Δх) ≈ f "(ξ) Δх + f(a),

kde bod x = a+ ξ sa nachádza na úsečke od x = a do x = a + Δx, hoci jeho presná poloha nie je známa. Presný vzorec umožňuje odhadnúť chybu približného vzorca. Ak do Lagrangeovho vzorca dáme ξ = Δx /2, tak hoci to prestáva byť presné, zvyčajne dáva oveľa lepšiu aproximáciu ako pôvodné vyjadrenie cez diferenciál.

Odhad chyby vzorcov pomocou diferenciálu

V zásade sú nepresné a vnášajú do nameraných údajov zodpovedajúce chyby. Vyznačujú sa hraničnou alebo skrátka maximálnou chybou - kladným číslom, ktoré je zjavne väčšie ako táto chyba v absolútnej hodnote (alebo v extrémnych prípadoch sa jej rovná). Limita je jej podiel vydelený absolútnou hodnotou meranej veličiny.

Nech sa na výpočet funkcie y použije presný vzorec y= f (x), ale hodnota x je výsledkom merania a preto vnáša do y chybu. Potom, aby ste našli maximálnu absolútnu chybu │‌‌Δу│funkcie y, použite vzorec

│‌‌Δу│≈│‌‌dy│=│ f "(x)││Δх│,

kde │Δх│je maximálna chyba argumentu. Hodnota │‌‌Δу│ by mala byť zaokrúhlená nahor, pretože Samotné nahradenie výpočtu prírastku výpočtom diferenciálu je nepresné.