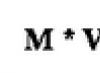Irrational expressions and their transformations
Last time we remembered (or learned, depending on who) what it is , learned how to extract such roots, sorted out the basic properties of roots piece by piece and solved simple examples with roots.
This lesson will be a continuation of the previous one and will be devoted to transformations of a wide variety of expressions containing all kinds of roots. Such expressions are called irrational. Expressions with letters, additional conditions, getting rid of irrationality in fractions, and some advanced techniques for working with roots will appear here. The techniques that will be discussed in this lesson will become a good basis for solving USE problems (and not only) of almost any level of complexity. So let's get started.
First of all, I will duplicate here the basic formulas and properties of roots. So as not to jump from topic to topic. Here they are:
![]()
![]() at
at
![]()
You must know these formulas and be able to apply them. And in both directions - both from left to right and from right to left. It is on them that the solution to most tasks with roots of any degree of complexity is based. Let's start with the simplest thing for now - with the direct application of formulas or their combinations.
Easy application of formulas
In this part, simple and harmless examples will be considered - without letters, additional conditions and other tricks. However, even in them, as a rule, there are options. And the more sophisticated the example, the more such options there are. And the inexperienced student faces the main problem - where to start? The answer here is simple - If you don't know what you need, do what you can. As long as your actions are in peace and harmony with the rules of mathematics and do not contradict them.) For example, this task:
Calculate:
Even in such a simple example, there are several possible paths to the answer.
The first is to simply multiply the roots by the first property and extract the root from the result:
The second option is this: we don’t touch it, we work with . We take the multiplier out from under the root sign, and then - according to the first property. Like this:
You can decide as much as you like. In any of the options, the answer is one - eight. For example, it’s easier for me to multiply 4 and 128 and get 512, and the cube root can be easily extracted from this number. If someone doesn’t remember that 512 is 8 cubed, then it doesn’t matter: you can write 512 as 2 9 (the first 10 powers of two, I hope you remember?) and using the formula for the root of the power:
Another example.
Calculate: .
If you work according to the first property (putting everything under one root), you will get a hefty number, from which the root can then be extracted - also not sugar. And it’s not a fact that it will be extracted exactly.) Therefore, it is useful here to remove the factors from under the root in the number. And make the most of:
And now everything is fine:
All that remains is to write the eight and two under one root (according to the first property) and the job is done. :)
Now let's add some fractions.
Calculate:
The example is quite primitive, but it also has options. You can use the multiplier to transform the numerator and reduce it with the denominator:

Or you can immediately use the formula for dividing roots:

As we see, this way and that way is correct.) If you don’t stumble halfway and make a mistake. Although where can I go wrong here...
Let's now look at the very last example from the homework of the last lesson:
Simplify:
![]()
A completely unimaginable set of roots, and even nested ones. What should I do? The main thing is not to be afraid! Here we first notice under the roots the numbers 2, 4 and 32 - powers of two. The first thing to do is to reduce all the numbers to twos: after all, the more identical numbers in the example and the fewer different ones, the easier it is.) Let’s start separately with the first factor:
![]()
The number can be simplified by reducing the two under the root with the four in the root exponent:
Now, according to the root of the work:
![]() .
.
In the number we take out the two as the root sign:
And we deal with the expression using the root of the root formula:
So, the first factor will be written like this:
The nested roots have disappeared, the numbers have become smaller, which is already pleasing. It’s just that the roots are different, but we’ll leave it that way for now. If necessary, we will convert them to the same ones. Let's take the second factor.)
We transform the second factor in a similar way, using the formula of the root of the product and the root of the root. Where necessary, we reduce the indicators using the fifth formula:
We paste everything into the original example and get:
We got the product of a whole bunch of completely different roots. It would be nice to bring them all to one indicator, and then we’ll see. Well, it's quite possible. The largest of the root exponents is 12, and all the others - 2, 3, 4, 6 - are divisors of the number 12. Therefore, we will reduce all roots according to the fifth property to one exponent - 12:
![]()
We count and get:
We didn’t get a nice number, but that’s okay. We were asked simplify expression, not count. Simplified? Certainly! And the type of answer (integer or not) no longer plays any role here.
Some addition/subtraction and abbreviated multiplication formulas
Unfortunately, general formulas for adding and subtracting roots no in mathematics. However, in tasks these actions with roots are often found. Here it is necessary to understand that any roots are exactly the same mathematical symbols as letters in algebra.) And the same techniques and rules apply to roots as to letters - opening parentheses, bringing similar ones, abbreviated multiplication formulas, etc. p.
For example, it is clear to everyone that . Exactly the same identical The roots can be added/subtracted to each other quite easily:
![]()
![]()
If the roots are different, then we look for a way to make them the same - by adding/subtracting a multiplier or using the fifth property. If it’s not simplified in any way, then perhaps the transformations are more cunning.
Let's look at the first example.
Find the meaning of the expression: .
All three roots, although cubic, are from different numbers. They are not purely extracted and are added/subtracted from each other. Therefore, the use of general formulas does not work here. What should I do? Let’s take out the factors in each root. In any case, it won’t be worse.) Moreover, there are, in fact, no other options:
Therefore, .
That's the solution. Here we moved from different roots to the same ones with the help removing the multiplier from under the root. And then they simply brought similar ones.) We decide further.
Find the value of an expression:
There's definitely nothing you can do about the root of seventeen. We work according to the first property - we make one root from the product of two roots:
Now let's take a closer look. What's under our big cube root? The difference is qua... Well, of course! Difference of squares:
Now all that remains is to extract the root: .
Calculate:
Here you will have to show mathematical ingenuity.) We think approximately as follows: “So, in the example, the product of roots. Under one root is the difference, and under the other is the sum. Very similar to the difference of squares formula. But... The roots are different! The first is square, and the second is of the fourth degree... It would be nice to make them the same. According to the fifth property, you can easily make a fourth root from a square root. To do this, it is enough to square the radical expression.”
If you thought about the same, then you are halfway to success. Absolutely right! Let's turn the first factor into a fourth root. Like this:
![]()
Now, there is nothing to be done, but you will have to remember the formula for the square of the difference. Only when applied to roots. So what? Why are roots worse than other numbers or expressions?! We build:
“Hmm, well, they erected it, so what? Horseradish is not sweeter than radish. Stop! And if you take out the four under the root? Then the same expression will emerge as under the second root, only with a minus, and this is exactly what we are trying to achieve!”
Right! Let's take four:
![]() .
.
And now - a matter of technology:
This is how complex examples are untangled.) Now it's time to practice with fractions.
Calculate:
It is clear that the numerator must be converted. How? Using the formula of the square of the sum, of course. Do we have any other options? :) We square it, take out the factors, reduce the indicators (where necessary):
Wow! We got exactly the denominator of our fraction.) This means that the whole fraction is obviously equal to one:

Another example. Only now on another formula for abbreviated multiplication.)
Calculate:
It is clear that the square of the difference must be used in practice. We write out the denominator separately and - let's go!
We take out the factors from under the roots:
![]()
Hence,
Now everything bad is superbly reduced and it turns out:

Well, let's take it to the next level. :)
Letters and additional conditions
Literal expressions with roots are a trickier thing than numerical expressions, and are an inexhaustible source of annoying and very serious errors. Let's close this source.) Errors arise due to the fact that such tasks often involve negative numbers and expressions. They are either given to us directly in the task, or hidden in letters and additional conditions. And in the process of working with roots, we constantly need to remember that in the roots even degree both under the root itself and as a result of extracting the root there should be non-negative expression. The key formula in the tasks of this paragraph will be the fourth formula:
There are no questions with roots of odd degrees - everything is always extracted, both positive and negative. And the minus, if anything, is brought forward. Let's get straight to the roots even degrees.) For example, such a short task.
Simplify: , If .
It would seem that everything is simple. It will just turn out to be X.) But why then the additional condition? In such cases, it is useful to estimate with numbers. Purely for myself.) If, then x is obviously a negative number. Minus three, for example. Or minus forty. Let . Can you raise minus three to the fourth power? Certainly! The result is 81. Is it possible to extract the fourth root of 81? Why not? Can! You get three. Now let's analyze our entire chain:
What do we see? The input was a negative number, and the output was already positive. It was minus three, now it’s plus three.) Let’s return to the letters. Without a doubt, modulo it will be exactly X, but only X itself is minus (by condition!), and the result of extraction (due to the arithmetic root!) must be plus. How to get a plus? Very simple! To do this, just put a minus in front of a obviously negative number.) And the correct solution looks like this:
By the way, if we used the formula, then, remembering the definition of a module, we would immediately get the correct answer. Since
|x| = -x at x<0.
Take the factor out of the root sign: , Where .
The first glance is at the radical expression. Everything is OK here. In any case, it will be non-negative. Let's start extracting. Using the formula for the root of a product, we extract the root of each factor:
I don’t think there’s any need to explain where the modules came from.) Now let’s analyze each of the modules.
Multiplier | a | we leave it unchanged: we don’t have any condition for the lettera. We don't know whether it's positive or negative. Next module |b 2 | can be safely omitted: in any case, the expressionb 2 non-negative. But about |c 3 | - there’s already a problem here.) If, then c 3 <0. Стало быть, модуль надо раскрыть with a minus: | c 3 | = - c 3 . In total, the correct solution would be:
And now - the reverse problem. Not the easiest, I warn you right away!
Enter a multiplier under the sign of the root: .
If you immediately write down the solution like this
then you fell into a trap. This wrong decision! What's the matter?
Let's take a closer look at the expression under the root. Under the root of the fourth degree, as we know, there should be non-negative expression. Otherwise, the root has no meaning.) Therefore And this, in turn, means that and, therefore, itself is also non-positive: .
And the mistake here is that we are introducing at the root non-positive number: the fourth degree turns it into non-negative and the wrong result is obtained - on the left there is a deliberate minus, and on the right there is already a plus. And apply at the root even degree we have the right only non-negative numbers or expressions. And leave the minus, if there is one, in front of the root.) How can we identify a non-negative factor in the number, knowing that it itself is completely negative? Yes, exactly the same! Put a minus.) And so that nothing changes, compensate for it with another minus. Like this:
![]()
And now already non-negative We calmly enter the number (-b) under the root according to all the rules:
This example clearly shows that, unlike other branches of mathematics, in the roots the correct answer does not always follow automatically from the formulas. You need to think and personally make the right decision.) You should especially be more careful with the signs in irrational equations and inequalities.
Let's look at the next important technique when working with roots - getting rid of irrationality.
Eliminating irrationality in fractions
If the expression contains roots, then, let me remind you, such an expression is called expression with irrationality. In some cases, it can be useful to get rid of this very irrationality (i.e. roots). How can you eliminate the root? Our root disappears when... raised to a power. With an indicator either equal to the root indicator or a multiple of it. But, if we raise the root to a power (i.e. multiply the root by itself the required number of times), then the expression will change. Not good.) However, in mathematics there are topics where multiplication is quite painless. In fractions, for example. According to the basic property of a fraction, if the numerator and denominator are multiplied (divided) by the same number, the value of the fraction will not change.
Let's say we are given this fraction:
Is it possible to get rid of the root in the denominator? Can! To do this, the root must be cubed. What are we missing in the denominator for a full cube? We are missing a multiplier, i.e.. So we multiply the numerator and denominator of the fraction by

The root in the denominator has disappeared. But... he appeared in the numerator. Nothing can be done, such is fate.) This is no longer important to us: we were asked to free the denominator from the roots. Released? Undoubtedly.)
By the way, those who are already comfortable with trigonometry may have paid attention to the fact that in some textbooks and tables, for example, they designate differently: somewhere , and somewhere . The question is - what is right? Answer: everything is correct!) If you guess that– this is simply the result of liberation from irrationality in the denominator of the fraction. :)
Why should we free ourselves from irrationality in fractions? What difference does it make - the root is in the numerator or in the denominator? The calculator will calculate everything anyway.) Well, for those who do not part with a calculator, there is really practically no difference... But even counting on a calculator, you can pay attention to the fact that divide on whole number is always more convenient and faster than on irrational. And I’ll keep silent about division into a column.)
The following example will only confirm my words.
How can we eliminate the square root of the denominator here? If the numerator and denominator are multiplied by the expression, then the denominator will be the square of the sum. The sum of the squares of the first and second numbers will give us just numbers without any roots, which is very pleasing. However... it will pop up double product the first number to the second, where the root of three will still remain. It doesn't channel. What should I do? Remember another wonderful formula for abbreviated multiplication! Where there are no double products, but only squares:
An expression that, when multiplied by a certain sum (or difference), produces difference of squares, also called conjugate expression. In our example, the conjugate expression will be the difference. So we multiply the numerator and denominator by this difference:
What can I say? As a result of our manipulations, not only did the root of the denominator disappear, but the fraction disappeared altogether! :) Even with a calculator, subtracting the root of three from a three is easier than calculating a fraction with the root in the denominator. Another example.
Free yourself from irrationality in the denominator of a fraction:
How to get out of this? Formulas for abbreviated multiplication with squares do not work right away - it will not be possible to completely eliminate the roots due to the fact that this time our root is not square, but cubic. It is necessary that the root is somehow raised into a cube. Therefore, one of the formulas with cubes must be used. Which one? Let's think about it. The denominator is the sum. How can we achieve the cube of the root? Multiply by partial squared difference! So, we will apply the formula sum of cubes. This one:
As a we have three, and as a quality b– cube root of five:
And again the fraction disappeared.) Such situations, when, when freed from irrationality in the denominator of a fraction, the fraction itself completely disappears along with the roots, occur very often. How do you like this example!
Calculate:
![]()
Just try adding these three fractions! No errors! :) One common denominator is worth it. What if we tried to free ourselves from the irrationality in the denominator of each fraction? Well, let's try:
Wow, how interesting! All the fractions are gone! Completely. And now the example can be solved in two ways:
Simple and elegant. And without long and tedious calculations. :)
That is why one must be able to do the operation of liberation from irrationality in fractions. In such sophisticated examples, it’s the only thing that saves, yes.) Of course, no one canceled attentiveness. There are tasks where you are asked to get rid of irrationality in numerator. These tasks are no different from those considered, only the numerator is cleared from the roots.)
More complex examples
It remains to consider some special techniques for working with roots and practice untangling not the simplest examples. And then the information received will be enough to solve tasks with roots of any level of complexity. So - go ahead.) First, let's figure out what to do with nested roots when the root from root formula does not work. For example, here's an example.
Calculate:
The root is under the root... Moreover, under the roots is the sum or difference. Therefore, the formula for the root of the root (with multiplication of exponents) is here doesn't work. So something needs to be done about radical expressions: We simply have no other options. In such examples, most often the large root is encrypted perfect square some amount. Or differences. And the root of a square can already be extracted perfectly! And now our task is to decrypt it.) Such decryption is beautifully done through system of equations. Now you will see everything for yourself.)
So, under the first root we have this expression:
What if you didn’t guess right? Let's check! We square it using the formula for the square of the sum:
That's right.) But... Where did I get this expression from? From the sky?
No.) We will get it a little lower honestly. Simply using this expression, I show exactly how task writers encrypt such squares. :) What is 54? This sum of squares of the first and second numbers. And, pay attention, already without roots! And the root remains in double product, which in our case is equal to . Therefore, unraveling such examples begins with searching for the double product. If you unravel with the usual selection. And, by the way, about signs. Everything is simple here. If there is a plus before the double, then the square of the sum. If it’s a minus, then the differences.) We have a plus – that means the square of the sum.) And now – the promised analytical method of decoding. Through the system.)
So, under our root there is clearly hanging out the expression (a+b) 2, and our task is to find a And b. In our case, the sum of squares gives 54. So we write:
![]()
Now double the product. We have it. So we write it down:
We got this system:
![]()
We solve by the usual substitution method. We express from the second equation, for example, and substitute it into the first:

Let's solve the first equation:
Received biquadratic equation relativea . We calculate the discriminant:
Means,
We got as many as four possible valuesa. We are not afraid. Now we will weed out all the unnecessary things.) If we now calculate the corresponding values for each of the four found values, we will get four solutions to our system. Here they are:
And here the question is - which solution is right for us? Let's think about it. Negative solutions can be immediately discarded: when squaring, the minuses will “burn out”, and the entire radical expression as a whole will not change.) The first two options remain. You can choose them completely arbitrarily: rearranging the terms still does not change the sum.) Let, for example, , a .
In total, we got the square of the following sum under the root:
Everything is clear.)
It’s not for nothing that I describe the decision process in such detail. To make it clear how decryption occurs.) But there is one problem. The analytical method of decoding, although reliable, is very long and cumbersome: you have to solve a biquadratic equation, get four solutions to the system and then still think about which ones to choose... Troubling? I agree, it's troublesome. This method works flawlessly in most of these examples. However, very often you can save yourself a lot of work and find both numbers creatively. By selection.) Yes, yes! Now, using the example of the second term (second root), I will show an easier and faster way to isolate the complete square under the root.
So now we have this root: ![]() .
.
Let's think like this: “Under the root is most likely an encrypted complete square. Once there is a minus before the double, it means the square of the difference. The sum of the squares of the first and second numbers gives us the number 54. But what kind of squares are these? 1 and 53? 49 and 5 ? There are too many options... No, it’s better to start untangling with double the product. Ourcan be written as . Times product doubled, then we immediately discard the two. Then candidates for the role a and b remain 7 and . What if it's 14 and/2 ? It's possible. But we always start with something simple!” So, let , a . Let's check them for the sum of squares:
It worked! This means that our radical expression is actually the square of the difference:
Here is a light way to avoid messing with the system. It doesn't always work, but in many of these examples it is quite sufficient. So, under the roots there are complete squares. All that remains is to correctly extract the roots and calculate the example:
Now let’s look at an even more non-standard task on roots.)
Prove that the number A– integer, if .
Nothing is directly extracted, the roots are embedded, and even of different degrees... A nightmare! However, the task makes sense.) Therefore, there is a key to solving it.) And the key here is this. Consider our equality
How equation relative A. Yes, yes! It would be nice to get rid of the roots. Our roots are cubic, so let’s cube both sides of the equation. According to the formula cube of the sum:

Cubes and cubic roots cancel each other out, and under each large root we take one bracket from the square and collapse the product of the difference and the sum into a difference of squares:
Separately, we calculate the difference of squares under the roots:
It's time to sort it out root extraction methods. They are based on the properties of roots, in particular, on the equality, which is true for any non-negative number b.
Below we will look at the main methods of extracting roots one by one.
Let's start with the simplest case - extracting roots from natural numbers using a table of squares, a table of cubes, etc.
If tables of squares, cubes, etc. If you don’t have it at hand, it’s logical to use the method of extracting the root, which involves decomposing the radical number into prime factors.
It is worth special mentioning what is possible for roots with odd exponents.
Finally, let's consider a method that allows us to sequentially find the digits of the root value.
Let's get started.
Using a table of squares, a table of cubes, etc.
In the simplest cases, tables of squares, cubes, etc. allow you to extract roots. What are these tables?
The table of squares of integers from 0 to 99 inclusive (shown below) consists of two zones. The first zone of the table is located on a gray background; by selecting a specific row and a specific column, it allows you to compose a number from 0 to 99. For example, let's select a row of 8 tens and a column of 3 units, with this we fixed the number 83. The second zone occupies the rest of the table. Each cell is located at the intersection of a certain row and a certain column, and contains the square of the corresponding number from 0 to 99. At the intersection of our chosen row of 8 tens and column 3 of ones there is a cell with the number 6,889, which is the square of the number 83.

Tables of cubes, tables of fourth powers of numbers from 0 to 99, and so on are similar to the table of squares, only they contain cubes, fourth powers, etc. in the second zone. corresponding numbers.
Tables of squares, cubes, fourth powers, etc. allow you to extract square roots, cube roots, fourth roots, etc. accordingly from the numbers in these tables. Let us explain the principle of their use when extracting roots.
Let's say we need to extract the nth root of the number a, while the number a is contained in the table of nth powers. Using this table we find the number b such that a=b n. Then ![]() , therefore, the number b will be the desired root of the nth degree.
, therefore, the number b will be the desired root of the nth degree.
As an example, let's show how to use a cube table to extract the cube root of 19,683. We find the number 19,683 in the table of cubes, from it we find that this number is the cube of the number 27, therefore, ![]() .
.

It is clear that tables of nth powers are very convenient for extracting roots. However, they are often not at hand, and compiling them requires some time. Moreover, it is often necessary to extract roots from numbers that are not contained in the corresponding tables. In these cases, you have to resort to other methods of root extraction.
Factoring a radical number into prime factors
A fairly convenient way to extract the root of a natural number (if, of course, the root is extracted) is to decompose the radical number into prime factors. His the point is this: after that it is quite easy to represent it as a power with the desired exponent, which allows you to obtain the value of the root. Let's clarify this point.
Let the nth root of a natural number a be taken and its value equal b. In this case, the equality a=b n is true. The number b, like any natural number, can be represented as the product of all its prime factors p 1 , p 2 , …, p m in the form p 1 ·p 2 ·…·p m , and the radical number a in this case is represented as (p 1 ·p 2 ·…·p m) n . Since the decomposition of a number into prime factors is unique, the decomposition of the radical number a into prime factors will have the form (p 1 ·p 2 ·…·p m) n, which makes it possible to calculate the value of the root as.
Note that if the decomposition into prime factors of a radical number a cannot be represented in the form (p 1 ·p 2 ·…·p m) n, then the nth root of such a number a is not completely extracted.
Let's figure this out when solving examples.
Example.
Take the square root of 144.
Solution.
If you look at the table of squares given in the previous paragraph, you can clearly see that 144 = 12 2, from which it is clear that the square root of 144 is 12.
But in light of this point, we are interested in how the root is extracted by decomposing the radical number 144 into prime factors. Let's look at this solution.
Let's decompose 144 to prime factors:
That is, 144=2·2·2·2·3·3. Based on the resulting decomposition, the following transformations can be carried out: 144=2·2·2·2·3·3=(2·2) 2·3 2 =(2·2·3) 2 =12 2. Hence, ![]() .
.
Using the properties of the degree and the properties of the roots, the solution could be formulated a little differently: .
Answer:
To consolidate the material, consider the solutions to two more examples.
Example.
Calculate the value of the root.
Solution.
The prime factorization of the radical number 243 has the form 243=3 5 . Thus, ![]() .
.
Answer:
Example.
Is the root value an integer?
Solution.
To answer this question, let's factor the radical number into prime factors and see if it can be represented as a cube of an integer.
We have 285 768=2 3 ·3 6 ·7 2. The resulting expansion cannot be represented as a cube of an integer, since the power of the prime factor 7 is not a multiple of three. Therefore, the cube root of 285,768 cannot be extracted completely.
Answer:
No.
Extracting roots from fractional numbers
It's time to figure out how to extract the root of a fractional number. Let the fractional radical number be written as p/q. According to the property of the root of a quotient, the following equality is true. From this equality it follows rule for extracting the root of a fraction: The root of a fraction is equal to the quotient of the root of the numerator divided by the root of the denominator.
Let's look at an example of extracting a root from a fraction.
Example.
What is the square root of the common fraction 25/169?
Solution.
Using the table of squares, we find that the square root of the numerator of the original fraction is equal to 5, and the square root of the denominator is equal to 13. Then  . This completes the extraction of the root of the common fraction 25/169.
. This completes the extraction of the root of the common fraction 25/169.
Answer:
The root of a decimal fraction or mixed number is extracted after replacing the radical numbers with ordinary fractions.
Example.
Take the cube root of the decimal fraction 474.552.
Solution.
Let's imagine the original decimal fraction as an ordinary fraction: 474.552=474552/1000. Then  . It remains to extract the cube roots that are in the numerator and denominator of the resulting fraction. Because 474 552=2·2·2·3·3·3·13·13·13=(2 3 13) 3 =78 3 and 1 000 = 10 3, then
. It remains to extract the cube roots that are in the numerator and denominator of the resulting fraction. Because 474 552=2·2·2·3·3·3·13·13·13=(2 3 13) 3 =78 3 and 1 000 = 10 3, then ![]() And
And ![]() . All that remains is to complete the calculations
. All that remains is to complete the calculations  .
.
Answer:
![]() .
.
Taking the root of a negative number
It is worthwhile to dwell on extracting roots from negative numbers. When studying roots, we said that when the root exponent is an odd number, then there can be a negative number under the root sign. We gave these entries the following meaning: for a negative number −a and an odd exponent of the root 2 n−1, ![]() . This equality gives rule for extracting odd roots from negative numbers: to extract the root of a negative number, you need to take the root of the opposite positive number, and put a minus sign in front of the result.
. This equality gives rule for extracting odd roots from negative numbers: to extract the root of a negative number, you need to take the root of the opposite positive number, and put a minus sign in front of the result.
Let's look at the example solution.
Example.
Find the value of the root.
Solution.
Let's transform the original expression so that there is a positive number under the root sign:  . Now replace the mixed number with an ordinary fraction:
. Now replace the mixed number with an ordinary fraction:  . We apply the rule for extracting the root of an ordinary fraction:
. We apply the rule for extracting the root of an ordinary fraction:  . It remains to calculate the roots in the numerator and denominator of the resulting fraction:
. It remains to calculate the roots in the numerator and denominator of the resulting fraction:  .
.
Here is a short summary of the solution:  .
.
Answer:
 .
.
Bitwise determination of the root value
In the general case, under the root there is a number that, using the techniques discussed above, cannot be represented as the nth power of any number. But in this case there is a need to know the meaning of a given root, at least up to a certain sign. In this case, to extract the root, you can use an algorithm that allows you to sequentially obtain a sufficient number of digit values of the desired number.
The first step of this algorithm is to find out what the most significant bit of the root value is. To do this, the numbers 0, 10, 100, ... are sequentially raised to the power n until the moment when a number exceeds the radical number is obtained. Then the number that we raised to the power n at the previous stage will indicate the corresponding most significant digit.
For example, consider this step of the algorithm when extracting the square root of five. We take the numbers 0, 10, 100, ... and square them until we get a number greater than 5. We have 0 2 =0<5 , 10 2 =100>5, which means the most significant digit will be the ones digit. The value of this bit, as well as the lower ones, will be found in the next steps of the root extraction algorithm.
All subsequent steps of the algorithm are aimed at sequentially clarifying the value of the root by finding the values of the next bits of the desired value of the root, starting with the highest one and moving to the lowest ones. For example, the value of the root at the first step turns out to be 2, at the second – 2.2, at the third – 2.23, and so on 2.236067977…. Let us describe how the values of the digits are found.
The digits are found by searching through their possible values 0, 1, 2, ..., 9. In this case, the nth powers of the corresponding numbers are calculated in parallel, and they are compared with the radical number. If at some stage the value of the degree exceeds the radical number, then the value of the digit corresponding to the previous value is considered found, and the transition is made to the next step of the root extraction algorithm; if this does not happen, then the value of this digit is equal to 9.
Let us explain these points using the same example of extracting the square root of five.
First we find the value of the units digit. We will go through the values 0, 1, 2, ..., 9, calculating 0 2, 1 2, ..., 9 2, respectively, until we get a value greater than the radical number 5. It is convenient to present all these calculations in the form of a table: 
So the value of the units digit is 2 (since 2 2<5
, а 2 3 >5). Let's move on to finding the value of the tenths place. In this case, we will square the numbers 2.0, 2.1, 2.2, ..., 2.9, comparing the resulting values with the radical number 5: 
Since 2.2 2<5
, а 2,3 2 >5, then the value of the tenths place is 2. You can proceed to finding the value of the hundredths place: 
This is how the next value of the root of five was found, it is equal to 2.23. And so you can continue to find values: 2,236, 2,2360, 2,23606, 2,236067, … .
To consolidate the material, we will analyze the extraction of the root with an accuracy of hundredths using the considered algorithm.
First we determine the most significant digit. To do this, we cube the numbers 0, 10, 100, etc. until we get a number greater than 2,151,186. We have 0 3 =0<2 151,186 , 10 3 =1 000<2151,186 , 100 3 =1 000 000>2 151.186, so the most significant digit is the tens digit.
Let's determine its value. 
Since 10 3<2 151,186
, а 20 3 >2 151.186, then the value of the tens place is 1. Let's move on to units. 
Thus, the value of the ones digit is 2. Let's move on to tenths. 
Since even 12.9 3 is less than the radical number 2 151.186, then the value of the tenths place is 9. It remains to perform the last step of the algorithm; it will give us the value of the root with the required accuracy. 
At this stage, the value of the root is found accurate to hundredths: ![]() .
.
In conclusion of this article, I would like to say that there are many other ways to extract roots. But for most tasks, the ones we studied above are sufficient.
References.
- Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: textbook for 8th grade. educational institutions.
- Kolmogorov A.N., Abramov A.M., Dudnitsyn Yu.P. and others. Algebra and the beginnings of analysis: Textbook for grades 10 - 11 of general education institutions.
- Gusev V.A., Mordkovich A.G. Mathematics (a manual for those entering technical schools).
Do you need to make complex calculations, but you don’t have an electronic computing device at hand? Use an online program - a root calculator. She will help:
- find square or cube roots of given numbers;
- perform mathematical operations with fractional powers.
| Number of decimal places: |
| √ |
How to calculate the square root manually - using the selection method to find suitable values. Let's look at how to do this.
What is square root
Root n powers of natural numbers a- number, n whose degree is equal a(radical number). The root is denoted by the symbol √. He is called a radical.
Every mathematical action has a reaction: addition→subtraction, multiplication→division, exponentiation→root.
Square root of a number a there will be a number whose square is equal to a. This implies the answer to the question, how to calculate the root of a number? You need to choose a number that to the second power will be equal to the value under the root.

Usually 2 is not written above the root sign. Since this is the smallest power, and accordingly, if there is no number, then the exponent is 2. We solve: to calculate the square root of 16, you need to find a number that, when raised to the second power, results in 16.

We carry out calculations manually
Calculations using the factorization method are performed in two ways, depending on the radical number:
1.An integer that can be factorized into squares and get an exact answer.
Square numbers are numbers from which the root can be extracted without leaving a remainder. And factors are numbers that, when multiplied, give the original number.
For example:
25, 36, 49 are square numbers because:

It turns out that square factors are factors that are square numbers.
Let's take 784 and extract the root from it.
| We factor the number into square factors. The number 784 is a multiple of 4, which means the first square factor is 4 x 4 = 16. Divide 784 by 16 and we get 49 - this is also a square number 7 x 7 = 16. |  |
| Let's apply the rule
We take the root of each square factor, multiply the results and get the answer. |
 Answer. |
2. Indivisible. It cannot be factorized into square factors.
Such examples occur more often than with integers. Their solution will not be exact, in other words, whole. It will be fractional and approximate. To simplify the problem, decomposing the radical number into a square factor and a number from which the square root cannot be extracted will help.
| We decompose the number 252 into a square and a regular factor. |  |
| We estimate the value of the root. To do this, we select two square numbers that stand in front and behind the radical number on the digital ruler. | The radical number is 7. This means that the nearest larger square number will be 8, and the smaller one will be 4.
|
| Assessing the value | Most likely, √7 is closer to 2. We select it in such a way that when this number is multiplied by itself, the result is 7. 2.7 x 2.7 = 7.2. Not suitable, since 7.2>7, take the smaller one 2.6 x 2.6 = 6.76. We leave it, because 6.76~7. |
| Calculate the root |  |
How to calculate the root of a complex number? Also using the method of estimating the values of the root.
When dividing into a column, the most accurate answer is obtained when extracting the root.
| Take a sheet of paper and draw it so that the vertical line is in the middle, and the horizontal line is on its right side and below the beginning. |  |
| Break the radical number into pairs of numbers. Decimal fractions are divided as follows: - whole part from right to left; — the number after the decimal point from left to right. |
Example: 3459842.825694 → 3 45 98 42, 82 56 94 795,28 → 7 95, 28 It is allowed that an unpaired number remains at the beginning. |
| For the first number (or pair), we select the largest number n. Its square must be less than or equal to the value of the first number (pair of numbers). Take the root √n from this number. Write the result on the top right, and the square of this number on the bottom right. Our first is 7. The nearest square number is 4. It is less than 7, and 4 = |
 |
| Subtract the found square of the number n from the first number (pair). Write the result under 7. And double the top number on the right and write the expression 4_x_=_ on the right. Note: the numbers must be the same. |
 |
| We select a number for the expression with dashes. To do this, find a number such that the resulting product is not greater than or equal to the current number on the left. In our case it is 8. |  |
| Write down the number you find in the upper right corner. This is the second number from the desired root. Take the next pair of numbers and write them down next to the resulting difference on the left. |
 |
| Subtract the product on the right from the number on the left. Double the number located at the top right and write the expression with dashes. |
 |
| We add a couple more numbers to the resulting difference. If these are numbers of the fractional part, that is, located behind a comma, then we put a comma in the upper right corner near the last digit of the desired square root. We fill in the dashes in the expression on the right, selecting the number so that the resulting product is less than or equal to the difference in the expression on the left. |
 |
| If you need more decimal places, then add next to the current number on the left and repeat the steps: subtract from the left, double the number in the upper right corner, write the expression with dashes, select factors for it, and so on. |  |
How much time do you think you will spend on such calculations? Difficult, long, confusing. Then why not make it easier for yourself? Use our program, which will help you make quick and accurate calculations.
Algorithm of actions
1. Enter the desired number of decimal places.
2. Indicate the degree of the root (if it is greater than 2).
3. Enter the number from which you plan to extract the root.
4. Click the "Solve" button.

Calculating the most complex mathematical operations with an online calculator will become simple!
To successfully use the root extraction operation in practice, you need to become familiar with the properties of this operation.
All properties are formulated and proven only for non-negative values of the variables contained under the signs of the roots.
Theorem 1. The nth root (n=2, 3, 4,...) of the product of two non-negative chips is equal to the product of the nth roots of these numbers:
Comment:
1.
Theorem 1 remains valid for the case when the radical expression is the product of more than two non-negative numbers.
Theorem 2.If,
and n is a natural number greater than 1, then the equality is true
Brief(albeit inaccurate) formulation, which is more convenient to use in practice: the root of a fraction is equal to the fraction of the roots.
Theorem 1 allows us to multiply t only roots of the same degree
, i.e. only roots with the same index.
Theorem 3.If ,k is a natural number and n is a natural number greater than 1, then the equality is true
In other words, to raise a root to a natural power, it is enough to raise the radical expression to this power.
This is a consequence of Theorem 1. In fact, for example, for k = 3 we obtain: We can reason in exactly the same way in the case of any other natural value of the exponent k.
Theorem 4.If ,k, n are natural numbers greater than 1, then the equality is true
In other words, to extract a root from a root, it is enough to multiply the indicators of the roots.
For example,
Be careful! We learned that four operations can be performed on roots: multiplication, division, exponentiation, and root extraction (from the root). But what about adding and subtracting roots? No way.
For example, instead of writing Really, But it’s obvious that
Theorem 5.If the indicators of the root and radical expression are multiplied or divided by the same natural number, then the value of the root will not change, i.e.
Examples of problem solving
Example 1. Calculate
Solution. Using the first property of roots (Theorem 1), we obtain:
Example 2. Calculate
Solution. Convert a mixed number to an improper fraction.
We have Using the second property of roots ( Theorem 2
), we get:
![]()
Example 3. Calculate: ![]()
Solution. Any formula in algebra, as you well know, is used not only “from left to right”, but also “from right to left”. Thus, the first property of roots means that they can be represented in the form and, conversely, can be replaced by the expression. The same applies to the second property of roots. Taking this into account, let's perform the calculations.
From this article you will learn:
- what is “root extraction”;
- in what cases is it removed;
- principles of finding the root value;
- basic methods of extracting roots from natural and fractional numbers.
What is "root extraction"
First, let’s introduce the definition of “root extraction.”
Definition 1
Root extraction is the process of finding the value of the root.
When we take the nth root of a number, we find the number b, the nth power of which is equal to a. If we find such a number b, we can say that the root has been extracted.
Note 1
The expressions “extracting the root” and “finding the value of the root” are equivalent.
In what cases is the root extracted?
Definition 2The nth root can be extracted from a number exactly if a can be represented as the nth power of some number b.
Example 1
4 = 2 × 2, therefore, the square root of the number 4 can be exactly taken, which is 2
Definition 3
When the n-th root of a number cannot be represented as the n-th power of b, then such a root not extracted or only approximate value is retrieved root accurate to any decimal place.
Example 2
2 ≈ 1 , 4142 .
Principles of finding root values and methods of extracting them
- Using a table of squares, a table of cubes, etc.
- Decomposition of a radical expression (number) into prime factors
- Taking the root of a negative number
It is necessary to understand by what principles the meaning of the roots is found and how they are extracted.
Definition 4
The main principle of finding the value of the roots is to be based on the properties of the roots, including the equality: b n n = b, which is valid for any non-negative number b.
You should start with the simplest and most obvious method: tables of squares, cubes, etc.
When you don’t have a table at hand, the method of decomposing a radical number into prime factors will help you (the method is simple).
It is worth paying attention to extracting the root of a negative number, which is possible for roots with odd exponents.
Let's learn how to take roots from fractions, including mixed numbers, fractions, and decimals.
And we will slowly consider the method of finding the value of the root bit by bit - the most complex and multi-stage one.
Using a table of squares, cubes, etc.
The table of squares includes all numbers from 0 to 99 and consists of 2 zones: in the first zone you can make any number up to 99 using a vertical column with tens and a horizontal row with units, the second zone contains all the squares of the numbers formed.
Table of squares
| Table of squares | units | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| tens | 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 | |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2041 | |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 | |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 | |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 | |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 | |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 | |
There are also tables of cubes, fourth powers, etc., which are created on a principle similar to the table of squares.
Cube table
| Cube table | units | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| tens | 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1 331 | 1 728 | 2 197 | 2 744 | 3 375 | 4 096 | 4 913 | 5 832 | 6 859 | |
| 2 | 8000 | 9 261 | 10 648 | 12 167 | 13 824 | 15 625 | 17 576 | 19 683 | 21 952 | 24 389 | |
| 3 | 27000 | 29 791 | 32 768 | 35 937 | 39 304 | 42 875 | 46 656 | 50 653 | 54 872 | 59 319 | |
| 4 | 64000 | 68 921 | 74 088 | 79 507 | 85 184 | 91 125 | 97 336 | 103 823 | 110 592 | 117 649 | |
| 5 | 125000 | 132 651 | 140 608 | 148 877 | 157 464 | 166 375 | 175 616 | 185 193 | 195 112 | 205 379 | |
| 6 | 216000 | 226 981 | 238 328 | 250 047 | 262 144 | 274 625 | 287 496 | 300 763 | 314 432 | 328 509 | |
| 7 | 343000 | 357 911 | 373 248 | 389 017 | 405 224 | 421 875 | 438 976 | 456 533 | 474 552 | 493 039 | |
| 8 | 512000 | 531 441 | 551 368 | 571 787 | 592 704 | 614 125 | 636 056 | 658 503 | 681 472 | 704 969 | |
| 729000 | 753 571 | 778 688 | 804 357 | 830 584 | 857 375 | 884 736 | 912 673 | 941 192 | 970 299 | ||
The operating principle of such tables is simple, but they are often not at hand, which greatly complicates the root extraction process, so you must know at least several methods of root extraction.
Factoring a radical number into prime factors
The most convenient way to find the root value after a table of squares and cubes.
Definition 5
The method of decomposing a radical number into prime factors involves representing the number as a power with the necessary exponent, which allows us to obtain the value of the root.
Example 3
Let's take the square root of 144.
Let's factor 144 into prime factors:
Thus: 144 = 2 × 2 × 2 × 2 × 3 × 3 = (2 × 2) 2 × 3 2 = (2 × 2 × 3) 2 = 12 2. Therefore, 144 = 12 2 = 12.
Also, when using the properties of powers and roots, you can write the transformation a little differently:
144 = 2 × 2 × 2 × 2 × 3 × 3 = 2 4 × 3 2 = 2 4 × 3 2 = 2 2 × 3 = 12
144 = 12 is the final answer.
Extracting roots from fractional numbers
Let's remember: Any fractional number must be written as a fraction.
Definition 6
Following the property of the root of a quotient, the following equality is valid:
p q n = p n q n . Based on this equality, it is necessary to use rule for extracting the root of a fraction: The root of a fraction is equal to the root of the numerator divided by the root of the denominator.
Example 4
Let's consider an example of extracting a root from a decimal fraction, since you can extract a root from an ordinary fraction using a table.
It is necessary to extract the cube root of 474, 552. First of all, let's imagine the decimal fraction as an ordinary fraction: 474, 552 = 474552 / 1000. From this it follows: 474552 1000 3 = 474552 3 1000 3. You can then begin the process of extracting the cube roots of the numerator and denominator:
474552 = 2 × 2 × 2 × 3 × 3 × 3 × 13 × 13 × 13 = (2 × 3 × 13) 3 = 78 3 and 1000 = 10 3, then
474552 3 = 78 3 3 = 78 and 1000 3 = 10 3 3 = 10.
We complete the calculations: 474552 3 1000 3 = 78 10 = 7, 8.
Rooting Negative Numbers
If the denominator is an odd number, then the number under the root sign may be negative. It follows from this: for a negative number - a and an odd exponent of the root 2 n - 1, the following equality holds:
A 2 × n - 1 = - a 2 × n - 1
Definition 7
Rule for extracting odd powers from negative numbers: To extract the root of a negative number, you need to take the root of the opposite positive number and put a minus sign in front of it.
Example 5
12 209 243 5. First, you need to transform the expression so that there is a positive number under the root sign:
12 209 243 5 = 12 209 243 - 5
Then you should replace the mixed number with an ordinary fraction:
12 209 243 - 5 = 3125 243 - 5
Using the rule for extracting roots from an ordinary fraction, we extract:
3125 243 - 5 = - 3125 5 243 5
We calculate the roots in the numerator and denominator:
3125 5 243 5 = - 5 5 5 3 5 5 = - 5 3 = - 1 2 3
Brief summary of the solution:
12 209 243 5 = 12 209 243 - 5 = 3125 243 - 5 = - 3125 5 243 5 = - 5 5 5 3 5 5 = - 5 3 = - 1 2 3 .
Answer: - 12 209 243 5 = - 1 2 3.
Bitwise determination of the root value
There are cases when under the root there is a number that cannot be represented as the nth power of a certain number. But it is necessary to know the value of the root accurate to a certain sign.
In this case, it is necessary to use an algorithm for finding the value of the root bitwise, with the help of which you can obtain a sufficient number of values of the desired number.
Example 6
Let's look at how this happens using the example of extracting the square root of 5.
First you need to find the value of the units digit. To do this, let's start going through the values 0, 1, 2, . . . , 9 , while calculating 0 2 , 1 2 , . . . , 9 2 to the required value, which is greater than the radical number 5. It is convenient to present all this in the form of a table:
The value of a series of units is 2 (since 2 2< 5 , а 2 3 >5) . Let's move to the category of tenths - we will square the numbers 2, 0, 2, 1, 2, 2, . . . , 2, 9, comparing the obtained values with the number 5.
Since 2, 2 2< 5 , а 2 , 3 2 >5, then the value of the tenths is 2. Let's move on to finding the value of hundredths:
Thus, the value of the root of five is found - 2, 23. You can find the root values further:
2 , 236 , 2 , 2360 , 2 , 23606 , 2 , 236067 , . . .
So, we have studied several of the most common ways to find the value of the root, which can be used in any situation.
If you notice an error in the text, please highlight it and press Ctrl+Enter




 between 2 and 4.
between 2 and 4.