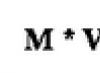Transformations of Admiral Makarov's puzzle (D. Vakarelov, A

Ministry of Education and Science Russian Federation

Sverdlovsk region

Tavdinsky urban district

MAOU average secondary school №2

Lesson development:

Puzzle making process

"Double Cross"

Chuprynin A.A.

technology teacher MAOU secondary school No. 2

Tavda

Topic: Making a puzzle

Cross (double) Makarov

Type of lesson: practical lesson

Practical work: Manufacturing of the product. Painting (varnishing) of products.

Objective of the lesson: Learn techniques for making wood products. Expand your knowledge of product finishing. Cultivating aesthetic taste and neat work skills.

Teaching methods: Explanation and demonstration of manufacturing and processing, finishing techniques, control, mutual training.

Interdisciplinary connections:mathematics, geometry, fine art.

Tasks:

Educational:

creating an idea of geometric shapes, materials used to manufacture the product;

formation of skills of sequential work in the manufacture of products using manual labor.

Educational:

development logical thinking and artistic taste.

Educational:

instilling accuracy in students' work;

formation of communication skills.

Cross (double) Makarov

This puzzle was designed by the famous admiral Makarov, the leader of two trips around the world.

Materials and tools:
Square block

Hacksaw or jigsaw

Square file

Flat file

Preparation for product manufacturing

Prepare six identical square blocks from the board.

To make the puzzle more compact and interesting, I recommend making it following sizes:

block length 60-80 mm square section 20 mm * 20 mm

One of them remains without cuts or sawing out (I).

On another block, away from the center of the block (not in the center), you need to cut out a groove with a hacksaw for metal or a jigsaw, a groove as wide as the thickness of the block and a depth of half this thickness (II).

On the third block, one groove is made in one direction from the center (you need to cut a groove the width of the block and the depth of half this thickness), and on the other side from the center, retreating half the thickness of the block, another one is as deep, but twice as narrow (III).

The remaining three blocks will be the same; on each of them two cuts are made: one with a width of two thicknesses of the block and a depth of half the thickness: the other, on the adjacent surface (for which the block is turned 90°), with a width of the thickness of the block and a depth of half the thickness (IV, V, VI).

Now all the blocks are ready for assembly

Now let's put the puzzle together.

Let's take two blocks of type IV, V, VI, fold them as shown in the figure.

Insert a block of type III into the resulting “window”.

Holding all three blocks so that they do not move apart, insert the remaining block of type IV, V, VI from above so that its thin part fits into the gap b, the uncut side

Next toIIItype II block must be placed with a block; turn it with the groove up and insert it from the side into the open “window” a.

If we look at the assembled figure formed by five blocks. Between the two blocks that we put together at the very beginning, a square “window” was preserved.

Into this “window” we introduce the remaining blockI(solid, without cutouts), then the entire structure will be firmly connected.

The cross is all assembled.

The world is designed in such a way that things in it can live longer than people, have different names V different times and in different countries. The toy you see in the picture is known in our country as the “Admiral Makarov puzzle.” In other countries it has other names, of which the most common are “devil’s cross” and “devil’s knot”.

This knot is connected from 6 square bars. The bars have grooves, thanks to which it is possible to cross the bars in the center of the knot. One of the bars does not have grooves; it is inserted into the assembly last, and when disassembled, it is removed first.

You can buy one of these puzzles, for example, on my-shop.ru

And also here various variations on the theme one, two, three, four, five, six, seven, eight.

The author of this puzzle is unknown. It appeared many centuries ago in China. In the Leningrad Museum of Anthropology and Ethnography named after. Peter the Great, known as the “Kunstkamera”, there is an ancient sandalwood box from India, in the 8 corners of which the intersections of the frame bars form 8 puzzles. In the Middle Ages, sailors and merchants, warriors and diplomats amused themselves with such puzzles and at the same time carried them around the world. Admiral Makarov, who visited China twice before his last trip and death in Port Arthur, brought the toy to St. Petersburg, where it became fashionable in secular salons. The puzzle also penetrated into the depths of Russia through other roads. It is known that the devil’s bundle was brought to the village of Olsufyevo, Bryansk region, by a soldier returning from the Russian-Turkish war.
Nowadays you can buy a puzzle in a store, but it’s more pleasant to make it yourself. Most suitable size bars for homemade design: 6x2x2 cm.

Variety of damn knots

Before the beginning of our century, over several hundred years of the toy’s existence, more than a hundred variants of the puzzle were invented in China, Mongolia and India, differing in the configuration of the cutouts in the bars. But two options remain the most popular. The one shown in Figure 1 is quite easy to solve; just make it. This is the design used in the ancient Indian box. The bars of Figure 2 are used to create a puzzle called the “Devil’s Knot.” As you might guess, it got its name due to the difficulty of solving it.

Rice. 1 The simplest option devil's knot puzzles

In Europe, where, starting from the end of the last century, the “Devil's Knot” became widely known, enthusiasts began to invent and make sets of bars with different cutout configurations. One of the most successful sets allows you to get 159 puzzles and consists of 20 bars of 18 types. Although all the nodes are externally indistinguishable, they are arranged completely differently inside.

Rice. 2 "Admiral Makarov's Puzzle"

Bulgarian artist, professor Petr Chukhovski, author of many bizarre and beautiful wooden knots from different quantities bruskov, also worked on the “Devil's Knot” puzzle. He developed a set of bar configurations and explored all possible combinations of 6 bars for one simple subset of it.

The most persistent of all in such searches was the Dutch mathematics professor Van de Boer, who with his own hands made a set of several hundred bars and compiled tables showing how to assemble 2906 variants of knots.

This was in the 60s, and in 1978, the American mathematician Bill Cutler wrote a computer program and, using exhaustive search, determined that there were 119,979 variants of a 6-piece puzzle, differing from each other in combinations of protrusions and depressions in the bars, as well as placement bars, provided that there are no voids inside the assembly.

Marvelous large number for such a small toy! Therefore, a computer was needed to solve the problem.

How does a computer solve puzzles?

Of course, not like a person, but not in some magical way either. The computer solves puzzles (and other problems) according to a program; programs are written by programmers. They write as they please, but in a way that the computer can understand. How does a computer manipulate wooden blocks?
We will assume that we have a set of 369 bars, differing from each other in the configurations of the protrusions (this set was first determined by Van de Boer). Descriptions of these bars must be entered into the computer. The minimum cutout (or protrusion) in a block is a cube with an edge equal to 0.5 of the thickness of the block. Let's call it a unit cube. The whole block contains 24 such cubes (Figure 1). In the computer, for each block, a “small” array of 6x2x2=24 numbers is created. A block with cutouts is specified by a sequence of 0s and 1s in a “small” array: 0 corresponds to a cutout cube, 1 to a whole one. Each of the “small” arrays has its own number (from 1 to 369). Each of them can be assigned a number from 1 to 6, corresponding to the position of the block inside the puzzle.

Let's move on to the puzzle now. Let's imagine that it fits inside a cube measuring 8x8x8. In a computer, this cube corresponds to a “large” array consisting of 8x8x8 = 512 number cells. Placing a certain block inside a cube means filling the corresponding cells of a “large” array with numbers equal to the number of a given block.

Comparing 6 “small” arrays and the main one, the computer (i.e., the program) seems to add 6 bars together. Based on the results of adding numbers, it determines how many and what “empty”, “filled” and “overcrowded” cells were formed in the main array. “Empty” cells correspond to empty space inside the puzzle, “filled” cells correspond to protrusions in the bars, and “crowded” cells correspond to an attempt to connect two single cubes together, which, of course, is prohibited. Such a comparison is made many times, not only with different bars, but also taking into account their turns, the places they occupy in the “cross”, etc.

As a result, those options are selected that do not have empty or overfilled cells. To solve this problem, a “large” array of 6x6x6 cells would be sufficient. It turns out, however, that there are combinations of bars that completely fill the internal volume of the puzzle, but it is impossible to disassemble them. Therefore, the program must be able to check the assembly for the possibility of disassembly. For this purpose, Cutler took an 8x8x8 array, although its dimensions may not be sufficient to test all cases.

It is filled with information about a specific version of the puzzle. Inside the array, the program tries to “move” the bars, that is, it moves parts of the bar with dimensions of 2x2x6 cells in the “large” array. The movement occurs by 1 cell in each of 6 directions, parallel to the axes of the puzzle. The results of those 6 attempts in which no “overfilled” cells are formed are remembered as starting points for the next six attempts. As a result, a tree of all possible movements is built until one block completely leaves the main array or, after all attempts, “overfilled” cells remain, which corresponds to an option that cannot be disassembled.

This is how 119,979 variants of the “Devil’s Knot” were obtained on a computer, including not 108, as the ancients believed, but 6402 variants, having 1 whole block without cuts.

Supernode

Please note that Cutler refused the study common task- when the node also contains internal voids. In this case, the number of nodes from 6 bars increases greatly and the exhaustive search required to find feasible solutions becomes unrealistic even for a modern computer. But as we will see now, the most interesting and difficult puzzles are contained precisely in the general case - disassembling the puzzle can then be made far from trivial.

Due to the presence of voids, it becomes possible to move several bars sequentially before one can be completely separated. A moving block unhooks some bars, allows the movement of the next block, and simultaneously engages other bars.
The more manipulations you need to do when disassembling, the more interesting and difficult the puzzle version. The grooves in the bars are arranged so cleverly that finding a solution resembles wandering through a dark labyrinth, in which you constantly come across walls or dead ends. This type of knot undoubtedly deserves a new name; we'll call it a "supernode". A measure of the complexity of a superknot is the number of movements of individual bars that must be made before the first element is separated from the puzzle.

We don't know who came up with the first supernode. The most famous (and most difficult to solve) are two superknots: the “Bill's Thorn” of difficulty 5, invented by W. Cutler, and the “Dubois Superknot” of difficulty 7. Until now, it was believed that the degree of difficulty 7 could hardly be surpassed. However, the first author of this article managed to improve the Dubois knot and increase the complexity to 9, and then, using some new ideas, get superknots with complexity 10, 11 and 12. But the number 13 remains insurmountable. Maybe the number 12 is the biggest difficulty of a supernode?

Supernode solution

To provide drawings of such difficult puzzles as superknots and not reveal their secrets would be too cruel to even puzzle experts. We will give the solution to superknots in a compact, algebraic form.

Before disassembling, we take the puzzle and orient it so that the part numbers correspond to Figure 1. The disassembly sequence is written down as a combination of numbers and letters. The numbers indicate the numbers of the bars, the letters indicate the direction of movement in accordance with the coordinate system shown in Figures 3 and 4. A line above a letter means movement in the negative direction of the coordinate axis. One step is to move the block 1/2 of its width. When a block moves two steps at once, its movement is written in brackets with an exponent of 2. If several parts that are interlocked are moved at once, then their numbers are enclosed in brackets, for example (1, 3, 6) x. The separation of the block from the puzzle is indicated by a vertical arrow.
Let us now give examples of the best supernodes.

W. Cutler's puzzle (“Bill's thorn”)

It consists of parts 1, 2, 3, 4, 5, 6, shown in Figure 3. An algorithm for solving it is also given there. Interestingly, the journal Scientific American (1985, No. 10) gives another version of this puzzle and reports that “Bill's thorn” has a unique solution. The difference between the options is in just one block: parts 2 and 2 B in Figure 3.

Rice. 3 "Bill's Thorn", developed with the help of a computer.

Due to the fact that part 2 B contains fewer cuts than part 2, it is not possible to insert it into the “Bill’s thorn” using the algorithm indicated in Figure 3. It remains to be assumed that the puzzle from Scientific American is assembled in some other way.

If this is the case and we assemble it, then after that we can replace part 2 B with part 2, since the latter takes up less volume than 2 B. As a result, we will get the second solution to the puzzle. But “Bill’s thorn” has a unique solution, and only one conclusion can be drawn from our contradiction: in the second version there was an error in the drawing.
A similar mistake was made in another publication (J. Slocum, J. Botermans “Puzzles old and new", 1986), but in a different block (detail 6 C in Figure 3). What was it like for those readers who tried, and perhaps are still trying, to solve these puzzles?

Puzzle by Philippe Dubois (Fig. 4)

It can be solved in 7 moves using the following algorithm: (6z)^2, 3x. 1z, 4x, 2x, 2y, 2z?. The figure shows the location of parts on the disassembly stage. Starting from this position, using the reverse order of the algorithm and changing the directions of movement to the opposite, you can assemble the puzzle.

Three supernodes by D. Vakarelova.

The first of his puzzles (Fig. 5) is an improved version of the Dubois puzzle, it has a difficulty of 9. This superknot is more like a labyrinth than others, since when disassembling it, false passages appear that lead to dead ends. An example of such a dead end is the moves 3x, 1z at the beginning of the showdown. A the right decision like this:

(6z)^2, 3x,1z, 4x, 2x, 2y, 5x, 5y, 3z?.

The second puzzle of D. Vakarelov (Fig. 6) is solved according to the formula:

4z,1z, 3x, 2x, 2z, 3x, 1z, 6z, 3x, 1x,3z?

and has a complexity of 11. It is remarkable in that block 3 takes the step Zx on the third move, and returns back on the sixth move (Zx); and block 1 at the second step moves along 1z, and at move 7 it makes a reverse move.

The third puzzle (Fig. 7) is one of the most difficult. Her solution:
4z, 1z, 3x, 2x, 2z, 3x, 6z, 1z, (1,3,6)x, 5y?
Until the seventh move, it repeats the previous puzzle, then, on the 9th move, a completely new situation is encountered: suddenly all the bars stop moving! And here you need to figure out how to move 3 bars at once (1, 3, 6), and if this movement is counted as 3 moves, then the complexity of the puzzle will be 12.

All photos from the article

Puzzles are known to develop intelligence, thinking and attentiveness well, so they are recommended for children to solve. True, some of them are not easy to cope with even for adults, who are also not averse to “twirling in their hands” funny details. In this article we will look at how to make some DIY wooden puzzles that will be fun for both children and adults to play with.

General information

First of all, it should be said that making wooden puzzles with your own hands is no less exciting than solving them. Moreover, there is nothing complicated in their manufacture, so anyone can cope with this task.

The only thing is that for this you will need a simple set of tools that every home craftsman has:

• Jigsaw (preferably a jigsaw);
• Chisels;
• Electric drill;
• Files and needle files;
• Sandpaper.

Advice!
To simplify the task and avoid mistakes in the process of making products, you first need to make drawings of wooden puzzles with your own hands.

As for materials, the most often required are:

• Small boards;
• Bars;
• Sheets of plywood;
• Wood varnish.

Even if these materials are not at hand, they can be purchased at hardware store. Their price is usually low.

Manufacturing

There are so many options for wooden puzzles for children and adults. Next we will look at the most popular and common of them, which are easy to do yourself.

To make this puzzle, you will need a rail whose width is three times the thickness, for example, if its thickness is 8 mm, then the width should be 24 mm.

The product is made as follows:

• A rail of suitable parameters must be cut into three parts of equal length.
• Next, in each plank you need to cut out a cutout corresponding to it with a jigsaw. cross section. As a result, the strips should fit into this hole with little effort. Therefore, it is better for the window to be slightly smaller; in this case, you can bring it to the required parameters using needle files.
• You need to make a cut in the two slats on the side, the width of which should be exactly equal to their thickness. As a result, a T-shaped cut should be obtained in two parts.
• At the end of the work, the parts need to be sanded and varnished.

This completes the puzzle making process.

Now you need to assemble it by following these steps:

• One of the parts with T-neck it must be inserted into the window, and it must be advanced so much that the end of the side cutout is “flush” with the surface of the strip.
• Next, you should take the third part and put it on top of the bar with the window until it stops.
• After this, you need to push down the first plank with a T-shaped cut all the way.

As a result, the puzzle takes the form of a single piece.

Crossroads

To complete this craft, you will need a 1 cm square block.

The instructions for its manufacture are as follows:

• You need to cut three bars about 8-9 centimeters long from the slats.
• In the middle of one of them, you need to make a cutout 1 cm wide so that you end up with a square jumper with sides of 0.5 cm.
• The second part should be made in exactly the same way, only the jumper should turn out not square, but round.
• In the third block you need to cut a groove 0.5 cm deep and wide.
• Then the same block must be rotated 90 degrees, and another similar groove must be made on the adjacent surface.
• Next, all parts should also be sanded and varnished.

The world is designed in such a way that things in it can live longer than people, have different names at different times and in different countries. The toy you see in the picture is known in our country as the “Admiral Makarov puzzle.” In other countries it has other names, of which the most common are “devil’s cross” and “devil’s knot”.

This knot is connected from 6 square bars. The bars have grooves, thanks to which it is possible to cross the bars in the center of the knot. One of the bars does not have grooves; it is inserted into the assembly last, and when disassembled, it is removed first.

The author of this puzzle is unknown. It appeared many centuries ago in China. In the Leningrad Museum of Anthropology and Ethnography named after. Peter the Great, known as the “Kunstkamera”, there is an ancient sandalwood box from India, in the 8 corners of which the intersections of the frame bars form 8 puzzles. In the Middle Ages, sailors and merchants, warriors and diplomats amused themselves with such puzzles and at the same time carried them around the world. Admiral Makarov, who visited China twice before his last trip and death in Port Arthur, brought the toy to St. Petersburg, where it became fashionable in secular salons. The puzzle also penetrated into the depths of Russia through other roads. It is known that the devil’s bundle was brought to the village of Olsufyevo in the Bryansk region by a soldier returning from the Russian-Turkish war.

Variety of damn knots

Before the beginning of our century, over several hundred years of the toy’s existence, more than a hundred variants of the puzzle were invented in China, Mongolia and India, differing in the configuration of the cutouts in the bars. But two options remain the most popular. The one shown in the first figure is quite easy to solve, just make it. This is the design used in the ancient Indian box. The bars of the second picture make up a puzzle called the “Devil’s Knot.” As you might guess, it got its name due to the difficulty of solving it.

In Europe, where, starting from the end of the last century, the “Devil's Knot” became widely known, enthusiasts began to invent and make sets of bars with different cutout configurations. One of the most successful sets allows you to get 159 puzzles and consists of 20 bars of 18 types. Although all the nodes are externally indistinguishable, they are arranged completely differently inside.

The Bulgarian artist, Professor Petr Chukhovski, the author of many bizarre and beautiful wooden knots from different numbers of bars, also worked on the “Devil's Knot” puzzle. He developed a set of bar configurations and explored all possible combinations of 6 bars for one simple subset of it.

The most persistent of all in such searches was the Dutch mathematics professor Van de Boer, who with his own hands made a set of several hundred bars and compiled tables showing how to assemble 2906 variants of knots.

This was in the 60s, and in 1978, the American mathematician Bill Cutler wrote a computer program and, using exhaustive search, determined that there were 119,979 variants of a 6-piece puzzle, differing from each other in combinations of protrusions and depressions in the bars, as well as placement bars, provided that there are no voids inside the assembly. Surprisingly large number for such a small toy! Therefore, a computer was needed to solve the problem.

How does a computer solve puzzles?

Of course, not like a person, but not in some magical way either. The computer solves puzzles (and other problems) according to a program; programs are written by programmers. They write as they please, but in a way that the computer can understand. How does a computer manipulate wooden blocks?

We will assume that we have a set of 369 bars, differing from each other in the configurations of the protrusions (this set was first determined by Van de Boer). Descriptions of these bars must be entered into the computer. The minimum cutout (or protrusion) in a block is a cube with an edge equal to 0.5 of the thickness of the block. Let's call it a unit cube. The whole block contains 24 such cubes. In the computer, for each block, a “small” array of 6x2x2=24 numbers is created. A block with cutouts is specified by a sequence of 0s and 1s in a “small” array: 0 corresponds to a cutout cube, 1 to a whole one. Each of the “small” arrays has its own number (from 1 to 369). Each of them can be assigned a number from 1 to 6, corresponding to the position of the block inside the puzzle.

Let's move on to the puzzle now. Let's imagine that it fits inside a cube measuring 8x8x8. In a computer, this cube corresponds to a “large” array consisting of 8x8x8 = 512 number cells. Placing a certain block inside a cube means filling the corresponding cells of a “large” array with numbers equal to the number of a given block.

Comparing 6 “small” arrays and the main one, the computer (i.e., the program) seems to add 6 bars together. Based on the results of adding numbers, it determines how many and what “empty”, “filled” and “overcrowded” cells were formed in the main array. “Empty” cells correspond to empty space inside the puzzle, “filled” cells correspond to protrusions in the bars, and “crowded” cells correspond to an attempt to connect two single cubes together, which, of course, is prohibited. Such a comparison is made many times, not only with different bars, but also taking into account their turns, the places they occupy in the “cross”, etc.

As a result, those options are selected that do not have empty or overfilled cells. To solve this problem, a “large” array of 6x6x6 cells would be sufficient. It turns out, however, that there are combinations of bars that completely fill the internal volume of the puzzle, but it is impossible to disassemble them. Therefore, the program must be able to check the assembly for the possibility of disassembly. For this purpose, Cutler took an 8x8x8 array, although its dimensions may not be sufficient to test all cases.

It is filled with information about a specific version of the puzzle. Inside the array, the program tries to “move” the bars, that is, it moves parts of the bar with dimensions of 2x2x6 cells in the “large” array. The movement occurs by 1 cell in each of 6 directions, parallel to the axes of the puzzle. The results of those 6 attempts in which no “overfilled” cells are formed are remembered as the starting positions for the next six attempts. As a result, a tree of all possible movements is built until one block completely leaves the main array or, after all attempts, “overfilled” cells remain, which corresponds to an option that cannot be disassembled.

This is how 119,979 variants of the “Devil’s Knot” were obtained on a computer, including not 108, as the ancients believed, but 6402 variants, having 1 whole block without cuts.

Supernode

Let us note that Cutler refused to study the general problem - when the node also contains internal voids. In this case, the number of nodes from 6 bars increases greatly and the exhaustive search required to find feasible solutions becomes unrealistic even for a modern computer. But as we will see now, the most interesting and difficult puzzles are contained precisely in the general case - disassembling the puzzle can then be made far from trivial.

Due to the presence of voids, it becomes possible to move several bars sequentially before one can be completely separated. A moving block unhooks some bars, allows the movement of the next block, and simultaneously engages other bars.

The more manipulations you need to do when disassembling, the more interesting and difficult the puzzle version. The grooves in the bars are arranged so cleverly that finding a solution resembles wandering through a dark labyrinth, in which you constantly come across walls or dead ends. This type of knot undoubtedly deserves a new name; we'll call it a "supernode". A measure of the complexity of a superknot is the number of movements of individual bars that must be made before the first element is separated from the puzzle.

We don't know who came up with the first supernode. The most famous (and most difficult to solve) are two superknots: the “Bill's Thorn” of difficulty 5, invented by W. Cutler, and the “Dubois Superknot” of difficulty 7. Until now, it was believed that the degree of difficulty 7 could hardly be surpassed. However, it was possible to improve the Dubois knot and increase the complexity to 9, and then, using some new ideas, get superknots with complexity 10, 11 and 12. But the number 13 remains insurmountable. Maybe the number 12 is the biggest difficulty of a supernode?

07.05.2013.

Knots of six bars.

I think I will not be mistaken if I say that the knot of six bars is the most famous wooden puzzle.

There is an opinion (and I completely share it!) that they were born wooden knots in Japan, as an improvisation on the theme of traditional local building structures. This is probably why modern residents of the Land of the Rising Sun are unsurpassed puzzlers. In the best sense of the word.

About ten years ago, armed with a rented machine that is unique to this day, children's creativity "Skillful hands", I made many versions of six-bar knots from oak and beech...

Regardless of the complexity of the original components, in all versions of this puzzle there is one straight, uncut block that is always inserted last into the structure and closes it into an inseparable whole.

The pages below from the already mentioned book by A.S. Pugachev show the variety of units of six bars and provide comprehensive information for their independent manufacture.

Among the options presented, some are very simple, and some are not very simple. Somehow it happened that one of them (in Pugachev’s book it appears as number 6) received its own name - “The Cross of Admiral Makarov.”

Knot of six bars - Puzzle "Cross of Admiral Makarov".

I won’t go into details why it’s called that - either because the glorious admiral, in the lulls between naval battles, loved to make it in ship’s carpentry, or for some other reason... I’ll just say one thing - this option is really difficult, despite the fact that the details lack the “internal” notches that I so dislike. It’s too inconvenient to pick them out with a chisel!

The images below, created using Autodesk 3D Max 3D modeling software, show appearance details and solution (sequence and orientation in space) of the puzzle "Cross of Admiral Makarov"

Among other things, in the same book by A.S. Pugachev there are drawings of other units, including those made of twelve and even sixteen bars!

A knot of sixteen bars.

Even though there are a lot of parts, this puzzle is quite simple to assemble. As in the case of six-bar units, the last part to be inserted is a straight piece without cutouts.