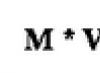Clean bend This type of bending is called in which the action takes place bending moment only(Fig. 3.5, A). Let us mentally draw the section plane I-I perpendicular to the longitudinal axis of the beam at a distance * from the free end of the beam to which the external moment is applied m z . Let us carry out actions similar to those that we performed when determining stresses and strains during torsion, namely:
- 1) let’s draw up equilibrium equations for the mentally cut-off part of the part;
- 2) we determine the deformation of the material of the part based on the conditions of compatibility of deformations of elementary volumes of a given section;
- 3) solve the equations of equilibrium and compatibility of deformations.
From the condition of equilibrium of the cut off section of the beam (Fig. 3.5, b)
we find that the moment of internal forces M z equal to the moment of external forces t: M = t.
Rice. 3.5.
The moment of internal forces is created by normal stresses o v directed along the x axis. With pure bending there are no external forces, therefore the sum of the projections of internal forces onto any coordinate axis is zero. On this basis, we write the equilibrium conditions in the form of equalities
Where A- cross-sectional area of the beam (rod).
In pure bending, external forces Fx, F, Fv as well as moments of external forces t x, t y are equal to zero. Therefore, the remaining equilibrium equations are identically equal to zero.
From the equilibrium condition 
when o^O it follows that
normal voltage c x in the cross section they take on both positive and negative values. (Experience shows that when bending the material of the lower side of the beam in Fig. 3.5, A stretched, and the upper one is compressed.) Consequently, in the cross section during bending there are such elementary volumes (of the transition layer from compression to tension) in which there is no elongation or compression. This - neutral layer. The line of intersection of the neutral layer with the cross-sectional plane is called neutral line.
The conditions for the compatibility of deformations of elementary volumes during bending are formed on the basis of the hypothesis of flat sections: the cross sections of the beam are flat before bending (see Fig. 3.5, b) will remain flat even after bending (Fig. 3.6).
As a result of the action of an external moment, the beam bends, and the section planes I-I and II-II rotate relative to each other at an angle dy(Fig. 3.6, b). In pure bending, the deformation of all sections along the beam axis is the same, therefore the radius pk of curvature of the neutral layer of the beam along the x axis is the same. Because dx= p K dip, then the curvature of the neutral layer is equal to 1 / p k = dip / dx and is constant along the length of the beam.
The neutral layer is not deformed; its length before and after deformation is equal to dx. Below this layer the material is stretched, above it is compressed.
Rice. 3.6.
The elongation value of the stretched layer located at a distance y from the neutral one is equal to ydq. Relative elongation of this layer:
Thus, in the adopted model, a linear distribution of deformations is obtained depending on the distance of a given elementary volume to the neutral layer, i.e. along the height of the beam section. Assuming that there is no mutual pressure of parallel layers of material on each other (o y = 0, a, = 0), we write Hooke’s law for linear stretching:
According to (3.13), normal stresses in the cross section of the beam are distributed according to a linear law. The stress of the elementary volume of the material farthest from the neutral layer (Fig. 3.6, V), maximum and equal 
? Problem 3.6
Determine the elastic limit of a steel blade with a thickness / = 4 mm and a length / = 80 cm, if its bending into a semicircle does not cause residual deformation.
Solution
Bending stress o v = Ey/ r k. Let's take y max = t/ 2i r k = / / To.
The elastic limit must correspond to the condition with уп > c v = 1 / 2 kE t /1.
Answer: o = ] / 2 to 2 10 11 4 10 _3 / 0.8 = 1570 MPa; The yield strength of this steel is a t > 1800 MPa, which exceeds the a t of the strongest spring steels. ?
? Problem 3.7
Determine the minimum radius of the drum for winding a tape with a thickness of / = 0.1 mm of a heating element made of a nickel alloy, at which the tape material is not plastically deformed. Module E= 1.6 10 5 MPa, elastic limit about yp = 200 MPa.
Answer: minimum radius р = V 2 ?ir/a yM = У? 1.6-10 11 0.1 10 -3 / (200 10 6) = = 0.04 m?
1. When solving the first equilibrium equation (3.12) and the deformation compatibility equation (3.13) together, we obtain 
Meaning E/ r k φ 0 and the same for all elements dA integration areas. Consequently, this equality is satisfied only under the condition
This integral is called static moment of cross-sectional area about the axisz? What is the physical meaning of this integral?
Let's take a plate of constant thickness /, but an arbitrary profile (Fig. 3.7). Let's hang this plate at a point WITH so that it is in a horizontal position. Let us denote by the symbol y m the specific gravity of the plate material, then the weight of the elementary volume with area dA equals dq= y JdA. Since the plate is in a state of equilibrium, then from the equality to zero of the projections of forces on the axis at we get
Where G= y M tA- weight of the record.
Rice. 3.7.
The sum of the moments of forces of all forces about the axis z passing through any section of the plate is also zero:
Considering that Yc = G, let's write down
Thus, if an integral of the form J xdA by area A equals
zero, then x c = 0. This means that point C coincides with the center of gravity of the plate. Therefore, from the equality S z = J ydA = 0 when due
bending it follows that the center of gravity of the cross section of the beam is on the neutral line.
Therefore, the value y s the cross section of the beam is zero.
- 1. The neutral line during bending passes through the center of gravity of the cross section of the beam.
- 2. The center of gravity of the cross section is the center of reduction of the moments of external and internal forces.
Problem 3.8
Problem 3.9
2. When solving the second equilibrium equation (3.12) and the deformation compatibility equation (3.13) together, we obtain
Integral Jz= J y 2 dA called moment of inertia of the transverse
section of the beam (rod) relative to the z axis, passing through the center of gravity of the cross section.
Thus, M z = E J z / r k. Considering that c x = Ee x = Ey/ r k i E/ r k = a x / y, we obtain the dependence of normal stresses Oh when bending:
1. The bending stress at a given point of the section does not depend on the normal elastic modulus E, but depends on the geometric parameter of the cross section Jz and distances at from a given point to the center of gravity of the cross section.
2. The maximum bending stress occurs in the elementary volumes furthest from the neutral line (see Fig. 3.6, V):
Where W z- moment of resistance of the cross section relative to the axis Z-
The condition for strength under pure bending is similar to the condition for strength under linear tension:
where [a m | - permissible bending stress.
It is obvious that the internal volumes of the material, especially near the neutral axis, are practically not loaded (see Fig. 3.6, V). This contradicts the requirement to minimize the material consumption of the structure. Below we will show some ways to overcome this contradiction.
Forces acting perpendicular to the axis of the beam and located in a plane passing through this axis cause deformation called transverse bending. If the plane of action of the mentioned forces – main plane, then a straight (flat) transverse bend occurs. Otherwise, the bend is called oblique transverse. A beam that is subject to predominantly bending is called beam 1 .
Essentially, transverse bending is a combination of pure bending and shear. In connection with the curvature of cross sections due to the uneven distribution of shears along the height, the question arises about the possibility of using the normal stress formula σ X, derived for pure bending based on the hypothesis of plane sections.
1 A single-span beam, having at the ends, respectively, one cylindrical fixed support and one cylindrical movable one in the direction of the beam axis, is called simple. A beam with one end clamped and the other free is called console. A simple beam having one or two parts hanging over a support is called console.
If, in addition, the sections are taken far from the places where the load is applied (at a distance not less than half the height of the section of the beam), then it can be assumed, as in the case of pure bending, that the fibers do not exert pressure on each other. This means that each fiber experiences uniaxial tension or compression.
Under the action of a distributed load, the transverse forces in two adjacent sections will differ by an amount equal to qdx. Therefore, the curvature of the sections will also be slightly different. In addition, the fibers will exert pressure on each other. A thorough study of the issue shows that if the length of the beam l quite large compared to its height h (l/ h> 5), then even with a distributed load, these factors do not have a significant effect on the normal stresses in the cross section and therefore may not be taken into account in practical calculations.
a B C
Rice. 10.5 Fig. 10.6
In sections under concentrated loads and near them, the distribution of σ X deviates from the linear law. This deviation, which is local in nature and is not accompanied by an increase in the highest stresses (in the outermost fibers), is usually not taken into account in practice.
Thus, with transverse bending (in the plane xy) normal stresses are calculated using the formula
σ X= – [M z(x)/Iz]y.
If we draw two adjacent sections on a section of the beam that is free from load, then the transverse force in both sections will be the same, and therefore the curvature of the sections will be the same. In this case, any piece of fiber ab(Fig. 10.5) will move to a new position a"b", without undergoing additional elongation, and therefore, without changing the value of the normal stress.
Let us determine the tangential stresses in the cross section through their paired stresses acting in the longitudinal section of the beam.
Select an element of length from the timber dx(Fig. 10.7 a). Let's draw a horizontal section at a distance at from neutral axis z, dividing the element into two parts (Fig. 10.7) and consider the equilibrium of the upper part, which has a base
width b. In accordance with the law of pairing of tangential stresses, the stresses acting in the longitudinal section are equal to the stresses acting in the cross section. Taking this into account, under the assumption that the shear stresses in the site b distributed uniformly, using the condition ΣХ = 0, we obtain:
N * - (N * +dN *)+
where: N * is the resultant of normal forces σ in the left cross section of the element dx within the “cut off” area A * (Fig. 10.7 d):
where: S = - static moment of the “cut off” part of the cross section (shaded area in Fig. 10.7 c). Therefore, we can write:
Then we can write:
This formula was obtained in the 19th century by the Russian scientist and engineer D.I. Zhuravsky and bears his name. And although this formula is approximate, since it averages the stress over the width of the section, the calculation results obtained from it are in good agreement with the experimental data.
In order to determine the shear stresses at an arbitrary cross-section point located at a distance y from the z axis, you should:
Determine from the diagram the magnitude of the transverse force Q acting in the section;
Calculate the moment of inertia I z of the entire section;
Draw a plane parallel to the plane through this point xz and determine the section width b;
Calculate the static moment of the clipped area S relative to the main central axis z and substitute the found values into the Zhuravsky formula.
Let us determine, as an example, tangential stresses in a rectangular cross section (Fig. 10.6, c). Static moment about the axis z parts of the section above line 1-1, on which the stress is determined, will be written in the form:
It varies according to the law of a square parabola. Section width V for a rectangular beam is constant, then the law of change in tangential stresses in the section will also be parabolic (Fig. 10.6, c). At y = and y = − the tangential stresses are zero, and on the neutral axis z they reach their greatest value.
For a beam of circular cross section on the neutral axis we have.
Bending is a type of deformation in which the longitudinal axis of the beam is bent. Straight beams that bend are called beams. Direct bending is a bend in which the external forces acting on the beam lie in one plane (force plane) passing through the longitudinal axis of the beam and the main central axis of inertia of the cross section.
The bend is called pure, if only one bending moment occurs in any cross section of the beam.
Bending, in which a bending moment and a transverse force simultaneously act in the cross section of a beam, is called transverse. The line of intersection of the force plane and the cross-sectional plane is called the force line.
Internal force factors during beam bending.
During plane transverse bending, two internal force factors arise in the beam sections: transverse force Q and bending moment M. To determine them, the method of sections is used (see lecture 1). The transverse force Q in the beam section is equal to the algebraic sum of the projections onto the section plane of all external forces acting on one side of the section under consideration.
Sign rule for shear forces Q:
The bending moment M in a beam section is equal to the algebraic sum of the moments relative to the center of gravity of this section of all external forces acting on one side of the section under consideration.
Sign rule for bending moments M:
Zhuravsky's differential dependencies.
Differential relationships have been established between the intensity q of the distributed load, the expressions for the transverse force Q and the bending moment M:
Based on these dependencies, the following general patterns of diagrams of transverse forces Q and bending moments M can be identified:
Features of diagrams of internal force factors during bending.
1. In the section of the beam where there is no distributed load, the diagram Q is presented straight line , parallel to the base of the diagram, and diagram M - an inclined straight line (Fig. a).
2. In the section where a concentrated force is applied, Q should be on the diagram leap , equal to the value of this force, and on the diagram M - breaking point (Fig. a).
3. In the section where a concentrated moment is applied, the value of Q does not change, and the diagram M has leap , equal to the value of this moment (Fig. 26, b).
4. In a section of a beam with a distributed load of intensity q, the diagram Q changes according to a linear law, and the diagram M changes according to a parabolic law, and the convexity of the parabola is directed towards the direction of the distributed load (Fig. c, d).
5. If, within a characteristic section, the diagram Q intersects the base of the diagram, then in the section where Q = 0, the bending moment has an extreme value M max or M min (Fig. d).
Normal bending stresses.
Determined by the formula:
The moment of resistance of a section to bending is the quantity:
Dangerous cross section during bending, the cross section of the beam in which the maximum normal stress occurs is called.
Shear stresses during straight bending.
Determined by Zhuravsky's formula for shear stresses during straight beam bending:
where S ots is the static moment of the transverse area of the cut-off layer of longitudinal fibers relative to the neutral line.
Calculations of bending strength.
1. At verification calculation The maximum design stress is determined and compared with the permissible stress:
2. At design calculation the selection of the beam section is made from the condition:
3. When determining the permissible load, the permissible bending moment is determined from the condition:
Bending movements.
Under the influence of bending load, the axis of the beam bends. In this case, tension of the fibers is observed on the convex part and compression on the concave part of the beam. In addition, there is a vertical movement of the centers of gravity of the cross sections and their rotation relative to the neutral axis. To characterize bending deformation, the following concepts are used:
Beam deflection Y- movement of the center of gravity of the cross section of the beam in the direction perpendicular to its axis.
Deflection is considered positive if the center of gravity moves upward. The amount of deflection varies along the length of the beam, i.e. y = y(z)
Section rotation angle- angle θ through which each section rotates relative to its original position. The rotation angle is considered positive when the section is rotated counterclockwise. The magnitude of the rotation angle varies along the length of the beam, being a function of θ = θ (z).
The most common methods for determining displacements is the method Mora And Vereshchagin's rule.
Mohr's method.
The procedure for determining displacements using Mohr's method:
1. An “auxiliary system” is built and loaded with a unit load at the point where the displacement is required to be determined. If linear displacement is determined, then a unit force is applied in its direction; when angular displacements are determined, a unit moment is applied.
2. For each section of the system, expressions for bending moments M f from the applied load and M 1 from the unit load are written down.
3. Over all sections of the system, Mohr’s integrals are calculated and summed, resulting in the desired displacement:
4. If the calculated displacement has a positive sign, this means that its direction coincides with the direction of the unit force. A negative sign indicates that the actual displacement is opposite to the direction of the unit force.
Vereshchagin's rule.
For the case when the diagram of bending moments from a given load has an arbitrary outline, and from a unit load – a rectilinear outline, it is convenient to use the graphic-analytical method, or Vereshchagin’s rule.
where A f is the area of the diagram of the bending moment M f from a given load; y c – ordinate of the diagram from a unit load under the center of gravity of the diagram M f; EI x is the section stiffness of the beam section. Calculations using this formula are made in sections, in each of which the straight-line diagram should be without fractures. The value (A f *y c) is considered positive if both diagrams are located on the same side of the beam, negative if they are located on different sides. A positive result of multiplying diagrams means that the direction of movement coincides with the direction of a unit force (or moment). A complex diagram M f should be divided into simple figures (the so-called “plot stratification” is used), for each of which it is easy to determine the ordinate of the center of gravity. In this case, the area of each figure is multiplied by the ordinate under its center of gravity.
Straight transverse bend occurs when all loads are applied perpendicular to the axis of the rod, lie in the same plane and, in addition, the plane of their action coincides with one of the main central axes of inertia of the section. Straight transverse bending refers to a simple type of resistance and is flat stress state, i.e. two principal stresses are non-zero. With this type of deformation, internal forces arise: shear force and bending moment. A special case of direct transverse bending is pure bend, with such resistance there are load areas within which the transverse force becomes zero and the bending moment is non-zero. In the cross sections of the rods during direct transverse bending, normal and tangential stresses arise. Stresses are a function of internal force, in this case normal stresses are a function of bending moment, and tangential stresses are a function of shear force. For direct transverse bending, several hypotheses are introduced:
1) The cross sections of the beam, flat before deformation, remain flat and orthogonal to the neutral layer after deformation (hypothesis of plane sections or J. Bernoulli’s hypothesis). This hypothesis is satisfied under pure bending and is violated when shear forces, shear stresses, and angular deformation occur.
2) There is no mutual pressure between the longitudinal layers (hypothesis of non-pressure of fibers). From this hypothesis it follows that longitudinal fibers experience uniaxial tension or compression, therefore, with pure bending, Hooke's law is valid.
A rod undergoing bending is called beam. When bending, one part of the fibers stretches, the other part contracts. The layer of fibers located between the stretched and compressed fibers is called neutral layer, it passes through the center of gravity of the sections. The line of its intersection with the cross section of the beam is called neutral axis. Based on the introduced hypotheses for pure bending, a formula was obtained for determining normal stresses, which is also used for direct transverse bending. The normal stress can be found using the linear relationship (1), in which the ratio of the bending moment to the axial moment of inertia ( 
) in a particular section is a constant value, and the distance ( y) along the ordinate axis from the center of gravity of the section to the point at which the stress is determined varies from 0 to
.
.
(1)
To determine the shear stress during bending in 1856. Russian engineer and bridge builder D.I. Zhuravsky became addicted
.
(2)
The shear stress in a particular section does not depend on the ratio of the transverse force to the axial moment of inertia ( 
), because this value does not change within one section, but depends on the ratio of the static moment of the area of the cut-off part to the width of the section at the level of the cut-off part ( 
).
When straight transverse bending occurs movements: deflections (v
) and rotation angles (Θ
)
. To determine them, use the equations of the initial parameters method (3), which are obtained by integrating the differential equation of the curved axis of the beam ( 
).
Here v 0 , Θ 0 ,M 0 , Q 0 – initial parameters, x – distance from the origin to the section in which the displacement is determined , a– the distance from the origin of coordinates to the place of application or the beginning of the load.
Strength and stiffness calculations are made using the strength and stiffness conditions. Using these conditions, you can solve verification problems (check the fulfillment of a condition), determine the size of the cross section, or select the permissible value of the load parameter. There are several strength conditions, some of which are given below. Normal stress strength condition has the form:
,
(4)
Here 
–
moment of resistance of the section relative to the z axis, R – design resistance based on normal stresses.
Strength condition for tangential stresses looks like:
,
(5)
here the notations are the same as in Zhuravsky’s formula, and R s – calculated shear resistance or calculated resistance to tangential stresses.
Strength condition according to the third strength hypothesis or the hypothesis of the greatest tangential stresses can be written in the following form:
.
(6)
Severity conditions can be written for deflections (v ) And rotation angles (Θ ) :
where the displacement values in square brackets are valid.
Example of completing individual task No. 4 (term 2-8 weeks)
Bend is called deformation in which the axis of the rod and all its fibers, i.e. longitudinal lines parallel to the axis of the rod, are bent under the influence of external forces. The simplest case of bending occurs when external forces lie in a plane passing through the central axis of the rod and do not produce projections onto this axis. This type of bending is called transverse bending. There are flat bends and oblique bends.
Flat bend- such a case when the curved axis of the rod is located in the same plane in which external forces act.
Oblique (complex) bend– a case of bending when the bent axis of the rod does not lie in the plane of action of external forces.
A bending rod is usually called beam.
During flat transverse bending of beams in a section with the coordinate system y0x, two internal forces can arise - transverse force Q y and bending moment M x; in what follows we introduce the notation for them Q And M. If there is no transverse force in a section or section of a beam (Q = 0), and the bending moment is not zero or M is const, then such a bend is usually called clean.
Lateral force in any section of the beam is numerically equal to the algebraic sum of the projections onto the axis of all forces (including support reactions) located on one side (either) of the drawn section.
Bending moment in a beam section is numerically equal to the algebraic sum of the moments of all forces (including support reactions) located on one side (any) of the drawn section relative to the center of gravity of this section, more precisely, relative to the axis passing perpendicular to the drawing plane through the center of gravity of the drawn section.
Force Q is resultant distributed over the cross-section of internal shear stress, A moment M– sum of moments around the central axis of section X internal normal stress.
There is a differential relationship between internal forces
which is used in constructing and checking Q and M diagrams.
Since some of the fibers of the beam are stretched, and some are compressed, and the transition from tension to compression occurs smoothly, without jumps, in the middle part of the beam there is a layer whose fibers only bend, but do not experience either tension or compression. This layer is called neutral layer. The line along which the neutral layer intersects the cross section of the beam is called neutral line th or neutral axis sections. Neutral lines are strung on the axis of the beam.
Lines drawn on the side surface of the beam perpendicular to the axis remain flat when bending. These experimental data make it possible to base the conclusions of the formulas on the hypothesis of plane sections. According to this hypothesis, the sections of the beam are flat and perpendicular to its axis before bending, remain flat and turn out to be perpendicular to the curved axis of the beam when it is bent. The cross section of the beam is distorted when bending. Due to transverse deformation, the cross-sectional dimensions in the compressed zone of the beam increase, and in the tensile zone they are compressed.
Assumptions for deriving formulas. Normal voltages
1) The hypothesis of plane sections is fulfilled.
2) Longitudinal fibers do not press on each other and, therefore, under the influence of normal stresses, linear tension or compression operates.
3) Deformations of fibers do not depend on their position along the cross-sectional width. Consequently, normal stresses, changing along the height of the section, remain the same along the width.
4) The beam has at least one plane of symmetry, and all external forces lie in this plane.
5) The material of the beam obeys Hooke's law, and the modulus of elasticity in tension and compression is the same.
6) The relationship between the dimensions of the beam is such that it operates in plane bending conditions without warping or twisting.
In case of pure bending of a beam, only normal stress, determined by the formula:
where y is the coordinate of an arbitrary section point, measured from the neutral line - the main central axis x.
Normal bending stresses along the height of the section are distributed over linear law. On the outermost fibers, normal stresses reach their maximum value, and at the center of gravity of the section they are equal to zero.
The nature of normal stress diagrams for symmetrical sections relative to the neutral line
The nature of normal stress diagrams for sections that do not have symmetry with respect to the neutral line
Dangerous points are the points furthest from the neutral line.
Let's choose some section
For any point of the section, let's call it a point TO, the beam strength condition for normal stresses has the form:
, where n.o. - This neutral axis
This axial section modulus relative to the neutral axis. Its dimension is cm 3, m 3. The moment of resistance characterizes the influence of the shape and dimensions of the cross section on the magnitude of the stresses.
Normal stress strength condition:
The normal stress is equal to the ratio of the maximum bending moment to the axial moment of resistance of the section relative to the neutral axis.
If the material does not equally resist tension and compression, then two strength conditions must be used: for the tensile zone with the permissible tensile stress; for a compression zone with permissible compressive stress.
During transverse bending, the beams on the platforms in its cross-section act as normal, so tangents voltage.
