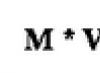1) The sum of the angles of a triangle is 180°.
Proof
Let "ABC" be an arbitrary triangle. Let us draw a straight line through vertex B, parallel to straight line AC (such a straight line is called the Euclidean straight line). Mark point D on it so that points A and D lie on opposite sides of straight line BC. Angles DBC and ACB are equal as interior lying crosswise, formed by the transversal BC with parallel lines AC and BD. Therefore, the sum of the angles of the triangle at vertices B and C is equal to the angle ABD. The sum of all three angles of the triangle is equal to the sum of the angles ABD and BAC Since these are one-sided interior angles for parallel AC and BD. secant AB, then their sum is equal to 180°.
2)
The exterior angle of a triangle at a given vertex is the angle adjacent to the angle of the triangle at this vertex.
Theorem: An exterior angle of a triangle is equal to the sum of two angles of the triangle that are not adjacent to it
Proof. Let ABC be the given triangle. By the theorem on the sum of angles in a triangle
∠ ABC + ∠ BCA + ∠ CAB = 180º.
this implies
∠ ABC + ∠ CAB = 180 º - ∠ BCA = ∠ BCD
The theorem has been proven.
From the theorem it follows:
An exterior angle of a triangle is greater than any angle of the triangle that is not adjacent to it.
3)
Sum of triangle angles = 180 degrees. If one of the angles is right (90 degrees) the other two are also 90. This means that each of them is less than 90, that is, they are acute. if one of the angles is obtuse, then the other two are less than 90, that is, they are clearly acute.
4)
obtuse - more than 90 degrees
acute - less than 90 degrees
5) a. A triangle in which one of the angles is 90 degrees.
b. Legs and hypotenuse
6)
6°. In each triangle, the larger angle lies opposite the larger side and vice versa: the larger angle lies opposite the larger angle. Any segment has one and only one midpoint.
7)
According to the Pythagorean theorem: the square of the hypotenuse is equal to the sum of the squares of the legs, which means the hypotenuse is greater than each of the legs
8) --- same as 7
9)
The sum of the angles of a triangle is 180 degrees. and if each side of the triangle were greater than the sum of the other two sides, then the sum of the angles would be greater than 180, which is impossible. Therefore, each side of the triangle is less than the sum of the other two sides.
10)
The sum of the angles of any triangle is 180 degrees.
Since this triangle is right-angled, one of its angles is right, i.e. equal to 90 degrees.
Therefore, the sum of the other two acute angles is 180-90=90 degrees.
11)
1. Consider a right triangle ABC in which angle A is a right angle, angle B = 30 degrees and angle C = 60. Let us attach to triangle ABC an equal triangle ABD. We get triangles BCD in which angle B = angle D = 60 degrees, therefore DC = BC. But according to the construction, AC is 1/2 BC, which is what needed to be proven.2. If the leg of a right triangle is equal to half the hypotenuse, then the angle opposite this leg is equal to 30 degrees. Let’s prove this. Consider a right triangle ABC, whose leg AC is equal to half the hypotenuse AC. Let us attach to triangle ABC an equal triangle ABD. Gets an equilateral triangle BCD. The angles of an equilateral triangle are equal to each other (since equal angles lie opposite equal sides), so each of them = 60 degrees. But angle DBC = 2 angles ABC, therefore angle ABC = 30 degrees, which is what needed to be proven.
“Tell me and I will forget,
Show me and I will remember
Involve me and I will learn”
Eastern proverb
Goal: Prove the theorem about the sum of the angles of a triangle, practice solving problems using this theorem, develop students’ cognitive activity using additional material from different sources, and develop the ability to listen to others.
Equipment: Protractor, ruler, triangle models, mood strip.
DURING THE CLASSES
1. Organizational moment.
Mark your mood at the beginning of the lesson on the mood tape.
2. Repetition.
Review the concepts that will be used in proving the theorem: properties of angles for parallel lines, definition of a straight angle, degree measure of a straight angle.
3. New material.
3.1. Practical work.
Each student has three models of a triangle: acute, rectangular and obtuse. It is proposed to measure the angles of a triangle and find their sum. Analyze the result. You can get values of 177, 178, 179, 180, 181, 182, 183 degrees. Calculate the arithmetic mean (=180°). It is suggested to remember when angles have a degree measure of 180 degrees. Students remember that this is a straight angle and the sum of one-sided angles.
Let's try to get the sum of the angles of a triangle using origami.
Historical reference
Origami (Japanese, lit.: “folded paper”) is the ancient art of folding paper figures. The art of origami has its roots in ancient China, where paper was discovered.
3.2. Proof of the theorem from the textbook by Atanasyan L.S.
Theorem on the sum of the angles of a triangle.
Let us prove one of the most important theorems of geometry - the theorem on the sum of the angles of a triangle.

Theorem. The sum of the angles of a triangle is 180°.
Proof. Consider an arbitrary triangle ABC and prove that A + B + C = 180°.
Let us draw a straight line a through vertex B, parallel to side AC. Angles 1 and 4 are cross-lying angles when parallel lines a and AC are intersected by secant AB, and angles 3 and 5 are cross-lying angles when the same parallel lines are intersected by secant BC. Therefore, angle 4 is equal to angle 1, angle 5 is equal to angle 3.
Obviously, the sum of angles 4, 2 and 5 is equal to the developed angle with vertex B, i.e. angle 4 + angle 2 + angle 5 = 180°. From here, taking into account the previous equalities, we obtain: angle 1 + angle 2+ angle 3 = 180°, or A + B+ C = 180°. The theorem has been proven.
3.3. Proof of the theorem from A. V. Pogorelov’s textbook.
Prove: A + B + C = 180°
Proof:
1. Draw a line BD // AC through vertex B
2. DBC=ACB, lying crosswise at AC//BD and secant BC.
3. ABD =ACB +CBD
Hence, A + B+C = ABD+BAC
4. ABD and BAC are one-sided with BD // AC and secant AB, which means their sum is equal to 180 °, i.e. A+B + C=180°, which is what needed to be proven.
3. 4. Proof of the theorem from the textbook by Kiselev A.N., Rybkina N.A.
Given: ABC
Prove: A+B +C=180°
Proof:
1. Let's continue the AC side. We will carry out SE//AV
2. A=ESD, as corresponding with AB//CE and AD - secant
3. B=ALL, lying crosswise at AB//CE and BC - the secant.
4. ESD + ALL + C = 180 °, which means A + B + C = 180 °, which was what needed to be proven.
3.5. Corollaries 1. In any triangle, all angles are acute, or two angles are acute, and the third is obtuse or straight.
Corollary 2.
An exterior angle of a triangle is equal to the sum of the other two angles of the triangle that are not adjacent to it.
3.6. The theorem allows us to classify triangles not only by sides, but also by angles.
| Triangle view | Isosceles | Equilateral | Versatile |
| rectangular |  |
||
| obtuse |  |
||
| acute-angled |
4. Consolidation.
4.1. Solving problems using ready-made drawings.
Find the unknown angles of the triangle.

4.2. Check of knowledge.
1. At the end of our lesson, answer the questions:
Are there triangles with angles:
a) 30, 60, 90 degrees,
b) 46, 4, 140 degrees,
c) 56, 46, 72 degrees?
2. Can a triangle have:
a) two obtuse angles,
b) obtuse and right angles,
c) two right angles?
3. Determine the type of triangle if one angle is 45 degrees, the other is 90 degrees.
4. In which triangle is the sum of the angles greater: acute, obtuse or rectangular?
5. Is it possible to measure the angles of any triangle?
This is a joke question, because... There is a Bermuda Triangle, located in the Atlantic Ocean between Bermuda, the state of Puerto Rico and the Florida Peninsula, whose angles cannot be measured. (Annex 1)
5. Lesson summary.
Mark your mood at the end of the lesson on the mood tape.
Homework.
P. 30–31; No. 223 a, b; No. 227 a; workbook no. 116, 118.
Theorem on the sum of interior angles of a triangle
The sum of the angles of a triangle is 180°.
Proof:
- Given triangle ABC.
- Through vertex B we draw a straight line DK parallel to the base AC.
- \angle CBK= \angle C as internal crosswise lying with parallel DK and AC, and secant BC.
- \angle DBA = \angle A internal crosswise lying with DK \parallel AC and secant AB. Angle DBK is reversed and equal to
- \angle DBK = \angle DBA + \angle B + \angle CBK
- Since the unfolded angle is equal to 180 ^\circ , and \angle CBK = \angle C and \angle DBA = \angle A , we get 180 ^\circ = \angle A + \angle B + \angle C.
The theorem is proven
Corollaries from the theorem on the sum of angles of a triangle:
- The sum of the acute angles of a right triangle is equal to 90°.
- In an isosceles right triangle, each acute angle is equal to 45°.
- In an equilateral triangle, each angle is equal 60°.
- In any triangle, either all the angles are acute, or two angles are acute, and the third is obtuse or right.
- An exterior angle of a triangle is equal to the sum of two interior angles that are not adjacent to it.
Triangle Exterior Angle Theorem
An exterior angle of a triangle is equal to the sum of the two remaining angles of the triangle that are not adjacent to this exterior angle
Proof:

- Given a triangle ABC, where BCD is the exterior angle.
- \angle BAC + \angle ABC +\angle BCA = 180^0
- From the equalities the angle \angle BCD + \angle BCA = 180^0
- We get \angle BCD = \angle BAC+\angle ABC.
Preliminary information
First, let's look directly at the concept of a triangle.
Definition 1
We will call a triangle a geometric figure that is made up of three points connected to each other by segments (Fig. 1).
Definition 2
Within the framework of Definition 1, we will call the points the vertices of the triangle.
Definition 3
Within the framework of Definition 1, we will call the segments sides of the triangle.
Obviously, any triangle will have 3 vertices, as well as three sides.
Theorem on the sum of angles in a triangle
Let us introduce and prove one of the main theorems related to triangles, namely the theorem on the sum of angles in a triangle.
Theorem 1
The sum of the angles in any arbitrary triangle is $180^\circ$.
Proof.
Consider the triangle $EGF$. Let us prove that the sum of the angles in this triangle is equal to $180^\circ$. Let's make an additional construction: draw the straight line $XY||EG$ (Fig. 2)
Since the lines $XY$ and $EG$ are parallel, then $∠E=∠XFE$ lie crosswise at the secant $FE$, and $∠G=∠YFG$ lie crosswise at the secant $FG$
Angle $XFY$ will be reversed and therefore equals $180^\circ$.
$∠XFY=∠XFE+∠F+∠YFG=180^\circ$
Hence
$∠E+∠F+∠G=180^\circ$
The theorem has been proven.
Triangle Exterior Angle Theorem
Another theorem on the sum of angles for a triangle can be considered the theorem on the external angle. First, let's introduce this concept.
Definition 4
We will call an external angle of a triangle an angle that will be adjacent to any angle of the triangle (Fig. 3).
Let us now consider the theorem directly.
Theorem 2
An exterior angle of a triangle is equal to the sum of two angles of the triangle that are not adjacent to it.
Proof.
Consider an arbitrary triangle $EFG$. Let it have an external angle of the triangle $FGQ$ (Fig. 3).
By Theorem 1, we will have that $∠E+∠F+∠G=180^\circ$, therefore,
$∠G=180^\circ-(∠E+∠F)$
Since the angle $FGQ$ is external, it is adjacent to the angle $∠G$, then
$∠FGQ=180^\circ-∠G=180^\circ-180^\circ+(∠E+∠F)=∠E+∠F$
The theorem has been proven.
Sample tasks
Example 1
Find all angles of a triangle if it is equilateral.
Since all the sides of an equilateral triangle are equal, we will have that all the angles in it are also equal to each other. Let us denote their degree measures by $α$.
Then, by Theorem 1 we get
$α+α+α=180^\circ$
Answer: all angles equal $60^\circ$.
Example 2
Find all angles of an isosceles triangle if one of its angles is equal to $100^\circ$.
Let us introduce the following notation for angles in an isosceles triangle:
Since we are not given in the condition exactly what angle $100^\circ$ is equal to, then two cases are possible:
An angle equal to $100^\circ$ is the angle at the base of the triangle.
Using the theorem on angles at the base of an isosceles triangle, we obtain
$∠2=∠3=100^\circ$
But then only their sum will be greater than $180^\circ$, which contradicts the conditions of Theorem 1. This means that this case does not occur.
An angle equal to $100^\circ$ is the angle between equal sides, that is