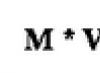General information about straight prism

The lateral surface of a prism (more precisely, the lateral surface area) is called sum areas of the side faces. The total surface of the prism is equal to the sum of the lateral surface and the areas of the bases.

Theorem 19.1. The lateral surface of a straight prism is equal to the product of the perimeter of the base and the height of the prism, i.e., the length of the side edge.

Proof. The lateral faces of a straight prism are rectangles. The bases of these rectangles are the sides of the polygon lying at the base of the prism, and the heights are equal to the length of the side edges. It follows that the lateral surface of the prism is equal to

S = a 1 l + a 2 l + ... + a n l = pl,

where a 1 and n are the lengths of the base edges, p is the perimeter of the base of the prism, and I is the length of the side edges. The theorem has been proven.

Practical task

Problem (22) . In an inclined prism it is carried out section, perpendicular to the side ribs and intersecting all the side ribs. Find the lateral surface of the prism if the perimeter of the section is equal to p and the side edges are equal to l.

Solution. The plane of the drawn section divides the prism into two parts (Fig. 411). Let us subject one of them to parallel translation, combining the bases of the prism. In this case, we obtain a straight prism, the base of which is the cross-section of the original prism, and the side edges are equal to l. This prism has the same lateral surface as the original one. Thus, the lateral surface of the original prism is equal to pl.

Summary of the covered topic

Now let’s try to summarize the topic we covered about prisms and remember what properties a prism has.

Prism properties

Firstly, a prism has all its bases as equal polygons;
Secondly, in a prism all its lateral faces are parallelograms;
Thirdly, in such a multifaceted figure as a prism, all lateral edges are equal;

Also, it should be remembered that polyhedra such as prisms can be straight or inclined.

Which prism is called a straight prism?

If the side edge of a prism is located perpendicular to the plane of its base, then such a prism is called a straight one.

It would not be superfluous to recall that the lateral faces of a straight prism are rectangles.

What type of prism is called oblique?

But if the side edge of a prism is not located perpendicular to the plane of its base, then we can safely say that it is an inclined prism.

Which prism is called correct?

If a regular polygon lies at the base of a straight prism, then such a prism is regular.

Now let's remember the properties that a regular prism has.

Properties of a regular prism

Firstly, regular polygons always serve as the bases of a regular prism;
Secondly, if we consider the side faces of a regular prism, they are always equal rectangles;
Thirdly, if you compare the sizes of the side ribs, then in a regular prism they are always equal.
Fourthly, a correct prism is always straight;
Fifthly, if in a regular prism the lateral faces have the shape of squares, then such a figure is usually called a semi-regular polygon.

Prism cross section

Now let's look at the cross section of the prism:

Homework

Now let's try to consolidate the topic we've learned by solving problems.

Let's draw an inclined triangular prism, the distance between its edges will be equal to: 3 cm, 4 cm and 5 cm, and the lateral surface of this prism will be equal to 60 cm2. Having these parameters, find the side edge of this prism.

Do you know that geometric figures constantly surround us, not only in geometry lessons, but also in everyday life there are objects that resemble one or another geometric figure.

Everyone at home, at school or at work has a computer whose system unit is shaped like a straight prism.

If you pick up a simple pencil, you will see that the main part of the pencil is a prism.

Walking along the central street of the city, we see that under our feet lies a tile that has the shape of a hexagonal prism.

A. V. Pogorelov, Geometry for grades 7-11, Textbook for educational institutions

Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.

Collection and use of personal information

Personal information refers to data that can be used to identify or contact a specific person.

You may be asked to provide your personal information at any time when you contact us.

Below are some examples of the types of personal information we may collect and how we may use such information.

What personal information do we collect:

• When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.

How we use your personal information:

• The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
• From time to time, we may use your personal information to send important notices and communications.
• We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
• If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.

Disclosure of information to third parties

We do not disclose the information received from you to third parties.

Exceptions:

• If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government authorities in the territory of the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
• In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.

Protection of personal information

We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.

Respecting your privacy at the company level

To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.

Polyhedra

The main object of study of stereometry is spatial bodies. Body represents a part of space limited by a certain surface.

Polyhedron is a body whose surface consists of a finite number of flat polygons. A polyhedron is called convex if it is located on one side of the plane of every plane polygon on its surface. The common part of such a plane and the surface of a polyhedron is called edge. The faces of a convex polyhedron are flat convex polygons. The sides of the faces are called edges of the polyhedron, and the vertices are vertices of the polyhedron.

For example, a cube consists of six squares, which are its faces. It contains 12 edges (the sides of the squares) and 8 vertices (the tops of the squares).

The simplest polyhedra are prisms and pyramids, which we will study further.

Prism

Definition and properties of a prism

Prism is a polyhedron consisting of two flat polygons lying in parallel planes combined by parallel translation, and all segments connecting the corresponding points of these polygons. Polygons are called prism bases, and the segments connecting the corresponding vertices of the polygons are lateral edges of the prism.

Prism height is called the distance between the planes of its bases (). A segment connecting two vertices of a prism that do not belong to the same face is called prism diagonal(). The prism is called n-carbon, if its base contains an n-gon.

Any prism has the following properties, resulting from the fact that the bases of the prism are combined by parallel translation:

1. The bases of the prism are equal.

2. The lateral edges of the prism are parallel and equal.

The surface of the prism consists of bases and lateral surface. The lateral surface of the prism consists of parallelograms (this follows from the properties of the prism). The area of ​​the lateral surface of a prism is the sum of the areas of the lateral faces.

Straight prism

The prism is called straight, if its lateral edges are perpendicular to the bases. Otherwise the prism is called inclined.

The faces of a right prism are rectangles. The height of a straight prism is equal to its side faces.

Full prism surface is called the sum of the lateral surface area and the areas of the bases.

With the right prism called a right prism with a regular polygon at its base.

Theorem 13.1. The area of ​​the lateral surface of a straight prism is equal to the product of the perimeter and the height of the prism (or, which is the same, by the lateral edge).

Proof. The lateral faces of a right prism are rectangles, the bases of which are the sides of the polygons at the bases of the prism, and the heights are the lateral edges of the prism. Then, by definition, the lateral surface area is:

,

where is the perimeter of the base of a straight prism.

Parallelepiped

If parallelograms lie at the bases of a prism, then it is called parallelepiped. All faces of a parallelepiped are parallelograms. In this case, the opposite faces of the parallelepiped are parallel and equal.

Theorem 13.2. The diagonals of a parallelepiped intersect at one point and are divided in half by the intersection point.

Proof. Consider two arbitrary diagonals, for example, and . Because the faces of a parallelepiped are parallelograms, then and , which means according to To there are two straight lines parallel to the third. In addition, this means that straight lines and lie in the same plane (plane). This plane intersects parallel planes and along parallel lines and . Thus, a quadrilateral is a parallelogram, and by the property of a parallelogram, its diagonals intersect and are divided in half by the intersection point, which was what needed to be proven.

A right parallelepiped whose base is a rectangle is called rectangular parallelepiped. All faces of a rectangular parallelepiped are rectangles. The lengths of the non-parallel edges of a rectangular parallelepiped are called its linear dimensions (dimensions). There are three such sizes (width, height, length).

Theorem 13.3. In a rectangular parallelepiped, the square of any diagonal is equal to the sum of the squares of its three dimensions (proven by applying Pythagorean T twice).

A rectangular parallelepiped with all edges equal is called cube.

Tasks

13.1 How many diagonals does it have? n-carbon prism

13.2 In an inclined triangular prism, the distances between the side edges are 37, 13 and 40. Find the distance between the larger side edge and the opposite side edge.

13.3 A plane is drawn through the side of the lower base of a regular triangular prism, intersecting the side faces along segments with an angle between them. Find the angle of inclination of this plane to the base of the prism.

Different prisms are different from each other. At the same time, they have a lot in common. To find the area of ​​the base of the prism, you will need to understand what type it has.

General theory

A prism is any polyhedron whose sides have the shape of a parallelogram. Moreover, its base can be any polyhedron - from a triangle to an n-gon. Moreover, the bases of the prism are always equal to each other. What does not apply to the side faces is that they can vary significantly in size.

When solving problems, not only the area of ​​the base of the prism is encountered. It may require knowledge of the lateral surface, that is, all the faces that are not bases. The complete surface will be the union of all the faces that make up the prism.

Sometimes problems involve height. It is perpendicular to the bases. The diagonal of a polyhedron is a segment that connects in pairs any two vertices that do not belong to the same face.

It should be noted that the base area of ​​a straight or inclined prism does not depend on the angle between them and the side faces. If they have the same figures on the top and bottom faces, then their areas will be equal.

Triangular prism

It has at its base a figure with three vertices, that is, a triangle. As you know, it can be different. If so, it is enough to remember that its area is determined by half the product of the legs.

The mathematical notation looks like this: S = ½ av.

To find out the area of ​​the base in general, the formulas are useful: Heron and the one in which half of the side is taken by the height drawn to it.

The first formula should be written as follows: S = √(р (р-а) (р-в) (р-с)). This notation contains a semi-perimeter (p), that is, the sum of three sides divided by two.

Second: S = ½ n a * a.

If you want to find out the area of ​​the base of a triangular prism, which is regular, then the triangle turns out to be equilateral. There is a formula for it: S = ¼ a 2 * √3.

Quadrangular prism

Its base is any of the known quadrangles. It can be a rectangle or square, parallelepiped or rhombus. In each case, in order to calculate the area of ​​the base of the prism, you will need your own formula.

If the base is a rectangle, then its area is determined as follows: S = ab, where a, b are the sides of the rectangle.

When it comes to a quadrangular prism, the area of ​​the base of a regular prism is calculated using the formula for a square. Because it is he who lies at the foundation. S = a 2.

In the case when the base is a parallelepiped, the following equality will be needed: S = a * n a. It happens that the side of a parallelepiped and one of the angles are given. Then, to calculate the height, you will need to use an additional formula: n a = b * sin A. Moreover, angle A is adjacent to side “b”, and height n is opposite to this angle.

If there is a rhombus at the base of the prism, then to determine its area you will need the same formula as for a parallelogram (since it is a special case of it). But you can also use this: S = ½ d 1 d 2. Here d 1 and d 2 are two diagonals of the rhombus.

Regular pentagonal prism

This case involves dividing the polygon into triangles, the areas of which are easier to find out. Although it happens that figures can have a different number of vertices.

Since the base of the prism is a regular pentagon, it can be divided into five equilateral triangles. Then the area of ​​the base of the prism is equal to the area of ​​one such triangle (the formula can be seen above), multiplied by five.

Regular hexagonal prism

Using the principle described for a pentagonal prism, it is possible to divide the hexagon of the base into 6 equilateral triangles. The formula for the base area of ​​such a prism is similar to the previous one. Only it should be multiplied by six.

The formula will look like this: S = 3/2 a 2 * √3.

Tasks

No. 1. Given a regular straight line, its diagonal is 22 cm, the height of the polyhedron is 14 cm. Calculate the area of ​​the base of the prism and the entire surface.

Solution. The base of the prism is a square, but its side is unknown. You can find its value from the diagonal of the square (x), which is related to the diagonal of the prism (d) and its height (h). x 2 = d 2 - n 2. On the other hand, this segment “x” is the hypotenuse in a triangle whose legs are equal to the side of the square. That is, x 2 = a 2 + a 2. Thus it turns out that a 2 = (d 2 - n 2)/2.

Substitute the number 22 instead of d, and replace “n” with its value - 14, it turns out that the side of the square is 12 cm. Now just find out the area of ​​the base: 12 * 12 = 144 cm 2.

To find out the area of ​​the entire surface, you need to add twice the base area and quadruple the side area. The latter can be easily found using the formula for a rectangle: multiply the height of the polyhedron and the side of the base. That is, 14 and 12, this number will be equal to 168 cm 2. The total surface area of ​​the prism turns out to be 960 cm 2.

Answer. The area of ​​the base of the prism is 144 cm 2. The entire surface is 960 cm 2.

No. 2. Given At the base there is a triangle with a side of 6 cm. In this case, the diagonal of the side face is 10 cm. Calculate the areas: the base and the side surface.

Solution. Since the prism is regular, its base is an equilateral triangle. Therefore, its area turns out to be equal to 6 squared, multiplied by ¼ and the square root of 3. A simple calculation leads to the result: 9√3 cm 2. This is the area of ​​one base of the prism.

All side faces are the same and are rectangles with sides of 6 and 10 cm. To calculate their areas, just multiply these numbers. Then multiply them by three, because the prism has exactly that many side faces. Then the area of ​​the lateral surface of the wound turns out to be 180 cm 2.

Answer. Areas: base - 9√3 cm 2, lateral surface of the prism - 180 cm 2.

Prism. Parallelepiped

Prism is a polyhedron whose two faces are equal n-gons (bases) , lying in parallel planes, and the remaining n faces are parallelograms (side faces) . Lateral rib The side of a prism that does not belong to the base is called the side of the prism.

A prism whose lateral edges are perpendicular to the planes of the bases is called straight prism (Fig. 1). If the side edges are not perpendicular to the planes of the bases, then the prism is called inclined . Correct A prism is a right prism whose bases are regular polygons.

Height prism is the distance between the planes of the bases. Diagonal A prism is a segment connecting two vertices that do not belong to the same face. Diagonal section is called a section of a prism by a plane passing through two lateral edges that do not belong to the same face. Perpendicular section is called a section of a prism by a plane perpendicular to the side edge of the prism.

Lateral surface area of a prism is the sum of the areas of all lateral faces. Total surface area is called the sum of the areas of all faces of the prism (i.e. the sum of the areas of the side faces and the areas of the bases).

For an arbitrary prism the following formulas are true::

Where l– length of the side rib;

H- height;

P

Q

S side

S full

S base– area of ​​the bases;

V– volume of the prism.

For a straight prism the following formulas are correct:

Where p– base perimeter;

l– length of the side rib;

H- height.

parallelepiped called a prism whose base is a parallelogram. A parallelepiped whose lateral edges are perpendicular to the bases is called direct (Fig. 2). If the side edges are not perpendicular to the bases, then the parallelepiped is called inclined . A right parallelepiped whose base is a rectangle is called rectangular. A rectangular parallelepiped with all edges equal is called cube

The faces of a parallelepiped that do not have common vertices are called opposite . The lengths of edges emanating from one vertex are called measurements parallelepiped. Since a parallelepiped is a prism, its main elements are defined in the same way as they are defined for prisms.

Theorems.

1. The diagonals of a parallelepiped intersect at one point and are bisected by it.

2. In a rectangular parallelepiped, the square of the length of the diagonal is equal to the sum of the squares of its three dimensions:

3. All four diagonals of a rectangular parallelepiped are equal to each other.

For an arbitrary parallelepiped the following formulas are valid:

Where l– length of the side rib;

H- height;

P– perpendicular section perimeter;

Q– Perpendicular cross-sectional area;

S side– lateral surface area;

S full– total surface area;

S base– area of ​​the bases;

V– volume of the prism.

For a right parallelepiped the following formulas are correct:

Where p– base perimeter;

l– length of the side rib;

H– height of a right parallelepiped.

For a rectangular parallelepiped the following formulas are correct:

(3)

Where p– base perimeter;

H- height;

d– diagonal;

a,b,c– measurements of a parallelepiped.

The following formulas are correct for a cube:

Where a– rib length;

d- diagonal of the cube.

Example 1. The diagonal of a rectangular parallelepiped is 33 dm, and its dimensions are in the ratio 2: 6: 9. Find the dimensions of the parallelepiped.

Solution. To find the dimensions of the parallelepiped, we use formula (3), i.e. by the fact that the square of the hypotenuse of a cuboid is equal to the sum of the squares of its dimensions. Let us denote by k proportionality factor. Then the dimensions of the parallelepiped will be equal to 2 k, 6k and 9 k. Let us write formula (3) for the problem data:

Solving this equation for k, we get:

This means that the dimensions of the parallelepiped are 6 dm, 18 dm and 27 dm.

Answer: 6 dm, 18 dm, 27 dm.

Example 2. Find the volume of an inclined triangular prism, the base of which is an equilateral triangle with a side of 8 cm, if the side edge is equal to the side of the base and inclined at an angle of 60º to the base.

Solution . Let's make a drawing (Fig. 3).

In order to find the volume of an inclined prism, you need to know the area of ​​its base and height. The area of ​​the base of this prism is the area of ​​an equilateral triangle with a side of 8 cm. Let us calculate it:

The height of a prism is the distance between its bases. From the top A 1 of the upper base, lower the perpendicular to the plane of the lower base A 1 D. Its length will be the height of the prism. Consider D A 1 AD: since this is the angle of inclination of the side edge A 1 A to the base plane, A 1 A= 8 cm. From this triangle we find A 1 D:

Now we calculate the volume using formula (1):

Answer: 192 cm 3.

Example 3. The lateral edge of a regular hexagonal prism is 14 cm. The area of ​​the largest diagonal section is 168 cm 2. Find the total surface area of ​​the prism.

Solution. Let's make a drawing (Fig. 4)

The largest diagonal section is a rectangle A.A. 1 DD 1 since diagonal AD regular hexagon ABCDEF is the largest. In order to calculate the lateral surface area of ​​the prism, it is necessary to know the side of the base and the length of the side edge.

Knowing the area of ​​the diagonal section (rectangle), we find the diagonal of the base.

Since then

Since then AB= 6 cm.

Then the perimeter of the base is:

Let us find the area of ​​the lateral surface of the prism:

The area of ​​a regular hexagon with side 6 cm is:

Find the total surface area of ​​the prism:

Answer:

Example 4. The base of a right parallelepiped is a rhombus. The diagonal cross-sectional areas are 300 cm2 and 875 cm2. Find the area of ​​the lateral surface of the parallelepiped.

Solution. Let's make a drawing (Fig. 5).

Let us denote the side of the rhombus by A, diagonals of a rhombus d 1 and d 2, parallelepiped height h. To find the area of ​​the lateral surface of a right parallelepiped, it is necessary to multiply the perimeter of the base by the height: (formula (2)). Base perimeter p = AB + BC + CD + DA = 4AB = 4a, because ABCD- rhombus H = AA 1 = h. That. Need to find A And h.

Let's consider diagonal sections. AA 1 SS 1 – a rectangle, one side of which is the diagonal of a rhombus AC = d 1, second – side edge AA 1 = h, Then

Similarly for the section BB 1 DD 1 we get:

Using the property of a parallelogram such that the sum of the squares of the diagonals is equal to the sum of the squares of all its sides, we obtain the equality We obtain the following.