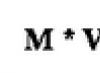Concept of area
The concept of the area of any geometric figure, in particular a triangle, will be associated with a figure such as a square. For the unit area of any geometric figure we will take the area of a square whose side is equal to one. For completeness, let us recall two basic properties for the concept of areas of geometric figures.
Property 1: If geometric figures are equal, then their areas are also equal.
Property 2: Any figure can be divided into several figures. Moreover, the area of the original figure is equal to the sum of the areas of all its constituent figures.
Let's look at an example.
Example 1
Obviously, one of the sides of the triangle is a diagonal of a rectangle, one side of which has a length of $5$ (since there are $5$ cells), and the other is $6$ (since there are $6$ cells). Therefore, the area of this triangle will be equal to half of such a rectangle. The area of the rectangle is
Then the area of the triangle is equal to
Answer: $15$.
Next, we will consider several methods for finding the areas of triangles, namely using the height and base, using Heron’s formula and the area of an equilateral triangle.
How to find the area of a triangle using its height and base
Theorem 1
The area of a triangle can be found as half the product of the length of a side and the height to that side.
Mathematically it looks like this
$S=\frac(1)(2)αh$
where $a$ is the length of the side, $h$ is the height drawn to it.
Proof.
Consider a triangle $ABC$ in which $AC=α$. The height $BH$ is drawn to this side, which is equal to $h$. Let's build it up to the square $AXYC$ as in Figure 2.

The area of rectangle $AXBH$ is $h\cdot AH$, and the area of rectangle $HBYC$ is $h\cdot HC$. Then
$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$
Therefore, the required area of the triangle, by property 2, is equal to
$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$
The theorem has been proven.
Example 2
Find the area of the triangle in the figure below if the cell has an area equal to one
The base of this triangle is equal to $9$ (since $9$ is $9$ squares). The height is also $9$. Then, by Theorem 1, we get
$S=\frac(1)(2)\cdot 9\cdot 9=40.5$
Answer: $40.5$.
Heron's formula
Theorem 2
If we are given three sides of a triangle $α$, $β$ and $γ$, then its area can be found as follows
$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
here $ρ$ means the semi-perimeter of this triangle.
Proof.
Consider the following figure:
By the Pythagorean theorem, from the triangle $ABH$ we obtain
From the triangle $CBH$, according to the Pythagorean theorem, we have
$h^2=α^2-(β-x)^2$
$h^2=α^2-β^2+2βx-x^2$
From these two relations we obtain the equality
$γ^2-x^2=α^2-β^2+2βx-x^2$
$x=\frac(γ^2-α^2+β^2)(2β)$
$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$
$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$
$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$
Since $ρ=\frac(α+β+γ)(2)$, then $α+β+γ=2ρ$, which means
$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$
$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$
$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$
$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
By Theorem 1, we get
$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
A triangle is a geometric figure that consists of three straight lines connecting at points that do not lie on the same straight line. The connection points of the lines are the vertices of the triangle, which are designated by Latin letters (for example, A, B, C). The connecting straight lines of a triangle are called segments, which are also usually denoted by Latin letters. The following types of triangles are distinguished:
- Rectangular.
- Obtuse.
- Acute angular.
- Versatile.
- Equilateral.
- Isosceles.
General formulas for calculating the area of a triangle
Formula for the area of a triangle based on length and height
S= a*h/2,
where a is the length of the side of the triangle whose area needs to be found, h is the length of the height drawn to the base.
Heron's formula
S=√р*(р-а)*(р-b)*(p-c),
where √ is the square root, p is the semi-perimeter of the triangle, a,b,c is the length of each side of the triangle. The semi-perimeter of a triangle can be calculated using the formula p=(a+b+c)/2.


Formula for the area of a triangle based on the angle and the length of the segment
S = (a*b*sin(α))/2,
where b,c is the length of the sides of the triangle, sin(α) is the sine of the angle between the two sides.


Formula for the area of a triangle given the radius of the inscribed circle and three sides
S=p*r,
where p is the semi-perimeter of the triangle whose area needs to be found, r is the radius of the circle inscribed in this triangle.


Formula for the area of a triangle based on three sides and the radius of the circle circumscribed around it
S= (a*b*c)/4*R,
where a,b,c is the length of each side of the triangle, R is the radius of the circle circumscribed around the triangle.


Formula for the area of a triangle using the Cartesian coordinates of points
Cartesian coordinates of points are coordinates in the xOy system, where x is the abscissa, y is the ordinate. The Cartesian coordinate system xOy on a plane is the mutually perpendicular numerical axes Ox and Oy with a common origin at point O. If the coordinates of points on this plane are given in the form A(x1, y1), B(x2, y2) and C(x3, y3 ), then you can calculate the area of the triangle using the following formula, which is obtained from the vector product of two vectors.
S = |(x1 – x3) (y2 – y3) – (x2 – x3) (y1 – y3)|/2,
where || stands for module.


How to find the area of a right triangle
A right triangle is a triangle with one angle measuring 90 degrees. A triangle can have only one such angle.
Formula for the area of a right triangle on two sides
S= a*b/2,
where a,b is the length of the legs. Legs are the sides adjacent to a right angle.


Formula for the area of a right triangle based on the hypotenuse and acute angle
S = a*b*sin(α)/ 2,
where a, b are the legs of the triangle, and sin(α) is the sine of the angle at which the lines a, b intersect.


Formula for the area of a right triangle based on the side and the opposite angle
S = a*b/2*tg(β),
where a, b are the legs of the triangle, tan(β) is the tangent of the angle at which the legs a, b are connected.


How to calculate the area of an isosceles triangle
An isosceles triangle is one that has two equal sides. These sides are called the sides, and the other side is the base. To calculate the area of an isosceles triangle, you can use one of the following formulas.
Basic formula for calculating the area of an isosceles triangle
S=h*c/2,
where c is the base of the triangle, h is the height of the triangle lowered to the base.


Formula of an isosceles triangle based on side and base
S=(c/2)* √(a*a – c*c/4),
where c is the base of the triangle, a is the size of one of the sides of the isosceles triangle.


How to find the area of an equilateral triangle
An equilateral triangle is a triangle in which all sides are equal. To calculate the area of an equilateral triangle, you can use the following formula:
S = (√3*a*a)/4,
where a is the length of the side of the equilateral triangle.


The above formulas will allow you to calculate the required area of the triangle. It is important to remember that to calculate the area of triangles, you need to consider the type of triangle and the available data that can be used for the calculation.
A triangle is the simplest geometric figure, which consists of three sides and three vertices. Due to its simplicity, the triangle has been used since ancient times to take various measurements, and today the figure can be useful for solving practical and everyday problems.
Features of a triangle
The figure has been used for calculations since ancient times, for example, land surveyors and astronomers operate with the properties of triangles to calculate areas and distances. It is easy to express the area of any n-gon through the area of this figure, and this property was used by ancient scientists to derive formulas for the areas of polygons. Constant work with triangles, especially the right triangle, became the basis for an entire branch of mathematics - trigonometry.
Triangle geometry
The properties of the geometric figure have been studied since ancient times: the earliest information about the triangle was found in Egyptian papyri from 4,000 years ago. Then the figure was studied in Ancient Greece and the greatest contributions to the geometry of the triangle were made by Euclid, Pythagoras and Heron. The study of the triangle never ceased, and in the 18th century, Leonhard Euler introduced the concept of the orthocenter of a figure and the Euler circle. At the turn of the 19th and 20th centuries, when it seemed that absolutely everything was known about the triangle, Frank Morley formulated the theorem on angle trisectors, and Waclaw Sierpinski proposed the fractal triangle.
There are several types of flat triangles that are familiar to us from school geometry courses:
- acute - all the corners of the figure are acute;
- obtuse - the figure has one obtuse angle (more than 90 degrees);
- rectangular - the figure contains one right angle equal to 90 degrees;
- isosceles - a triangle with two equal sides;
- equilateral - a triangle with all equal sides.
- There are all kinds of triangles in real life, and in some cases we may need to calculate the area of a geometric figure.
Area of a triangle
Area is an estimate of how much of the plane a figure encloses. The area of a triangle can be found in six ways, using the sides, height, angles, radius of the inscribed or circumscribed circle, as well as using Heron's formula or calculating the double integral along the lines bounding the plane. The simplest formula for calculating the area of a triangle is:
where a is the side of the triangle, h is its height.
However, in practice it is not always convenient for us to find the height of a geometric figure. The algorithm of our calculator allows you to calculate the area knowing:
- three sides;
- two sides and the angle between them;
- one side and two corners.
To determine the area through three sides, we use Heron's formula:
S = sqrt (p × (p-a) × (p-b) × (p-c)),
where p is the semi-perimeter of the triangle.
The area on two sides and an angle is calculated using the classic formula:
S = a × b × sin(alfa),
where alfa is the angle between sides a and b.
To determine the area in terms of one side and two angles, we use the relationship that:
a / sin(alfa) = b / sin(beta) = c / sin(gamma)
Using a simple proportion, we determine the length of the second side, after which we calculate the area using the formula S = a × b × sin(alfa). This algorithm is fully automated and you only need to enter the specified variables and get the result. Let's look at a couple of examples.
Examples from life
Paving slabs
Let's say you want to pave the floor with triangular tiles, and to determine the amount of material needed, you need to know the area of \u200b\u200bone tile and the area of the floor. Suppose you need to process 6 square meters of surface using a tile whose dimensions are a = 20 cm, b = 21 cm, c = 29 cm. Obviously, to calculate the area of a triangle, the calculator uses Heron’s formula and gives the result:
Thus, the area of one tile element will be 0.021 square meters, and you will need 6/0.021 = 285 triangles for the floor improvement. The numbers 20, 21 and 29 form a Pythagorean triple - numbers that satisfy . And that's right, our calculator also calculated all the angles of the triangle, and the gamma angle is exactly 90 degrees.
School task
In a school problem, you need to find the area of a triangle, knowing that side a = 5 cm, and angles alpha and beta are 30 and 50 degrees, respectively. To solve this problem manually, we would first find the value of side b using the proportion of the aspect ratio and the sines of the opposite angles, and then determine the area using the simple formula S = a × b × sin(alfa). Let's save time, enter the data into the calculator form and get an instant answer
When using the calculator, it is important to indicate the angles and sides correctly, otherwise the result will be incorrect.
Conclusion
The triangle is a unique figure that is found both in real life and in abstract calculations. Use our online calculator to determine the area of triangles of any kind.
Area of a triangle. In many geometry problems involving the calculation of areas, formulas for the area of a triangle are used. There are several of them, here we will look at the main ones.Listing these formulas would be too simple and of no use. We will analyze the origin of the basic formulas, those that are used most often.
Before you read the derivation of the formulas, be sure to look at the article about.After studying the material, you can easily restore the formulas in your memory (if they suddenly “fly out” at the moment you need).
First formula
The diagonal of a parallelogram divides it into two triangles of equal area:

Therefore, the area of the triangle will be equal to half the area of the parallelogram:

Area of triangle formula
*That is, if we know any side of the triangle and the height lowered to this side, then we can always calculate the area of this triangle.
Formula two
As already stated in the article on the area of a parallelogram, the formula looks like:

The area of a triangle is equal to half its area, which means:

*That is, if any two sides in a triangle and the angle between them are known, we can always calculate the area of such a triangle.
Heron's formula (third)

This formula is difficult to derive and it is of no use to you. Look how beautiful she is, you can say that she herself is memorable.
*If three sides of a triangle are given, then using this formula we can always calculate its area.
Formula four

Where r– radius of the inscribed circle
*If the three sides of a triangle and the radius of the circle inscribed in it are known, then we can always find the area of this triangle.
Formula five

Where R– radius of the circumscribed circle.
*If the three sides of a triangle and the radius of the circle circumscribed around it are known, then we can always find the area of such a triangle.
The question arises: if three sides of a triangle are known, then isn’t it easier to find its area using Heron’s formula!
Yes, it can be easier, but not always, sometimes complexity arises. This involves extracting the root. In addition, these formulas are very convenient to use in problems where the area of a triangle and its sides are given and you need to find the radius of the inscribed or circumscribed circle. Such tasks are available as part of the Unified State Exam.
Let's look at the formula separately:

It is a special case of the formula for the area of a polygon into which a circle is inscribed:
Let's consider it using the example of a pentagon:

Let us connect the center of the circle with the vertices of this pentagon and lower perpendiculars from the center to its sides. We get five triangles, with the dropped perpendiculars being the radii of the inscribed circle:

The area of the pentagon is:

Now it is clear that if we are talking about a triangle, then this formula takes the form:

Formula six
Sometimes in life there are situations when you have to delve into your memory in search of long-forgotten school knowledge. For example, you need to determine the area of a triangular-shaped plot of land, or the time has come for another renovation in an apartment or private house, and you need to calculate how much material will be needed for a surface with a triangular shape. There was a time when you could solve such a problem in a couple of minutes, but now you are desperately trying to remember how to determine the area of a triangle?
Don't worry about it! After all, it is quite normal when a person’s brain decides to transfer long-unused knowledge somewhere to a remote corner, from which sometimes it is not so easy to extract it. So that you don’t have to struggle with searching for forgotten school knowledge to solve such a problem, this article contains various methods that make it easy to find the required area of a triangle.
It is well known that a triangle is a type of polygon that is limited to the minimum possible number of sides. In principle, any polygon can be divided into several triangles by connecting its vertices with segments that do not intersect its sides. Therefore, knowing the triangle, you can calculate the area of almost any figure.
Among all the possible triangles that occur in life, the following particular types can be distinguished: and rectangular.
The easiest way to calculate the area of a triangle is when one of its angles is right, that is, in the case of a right triangle. It is easy to see that it is half a rectangle. Therefore, its area is equal to half the product of the sides that form a right angle with each other.
If we know the height of a triangle, lowered from one of its vertices to the opposite side, and the length of this side, which is called the base, then the area is calculated as half the product of the height and the base. This is written using the following formula:
S = 1/2*b*h, in which
S is the required area of the triangle;
b, h - respectively, the height and base of the triangle.
It is so easy to calculate the area of an isosceles triangle because the height will bisect the opposite side and can be easily measured. If the area is determined, then it is convenient to take the length of one of the sides forming a right angle as the height.
All this is of course good, but how to determine whether one of the angles of a triangle is right or not? If the size of our figure is small, then we can use a construction angle, a drawing triangle, a postcard or another object with a rectangular shape.
But what if we have a triangular plot of land? In this case, proceed as follows: count from the top of the supposed right angle on one side a distance multiple of 3 (30 cm, 90 cm, 3 m), and on the other side measure a distance multiple of 4 in the same proportion (40 cm, 160 cm, 4 m). Now you need to measure the distance between the end points of these two segments. If the result is a multiple of 5 (50 cm, 250 cm, 5 m), then we can say that the angle is right.
If the length of each of the three sides of our figure is known, then the area of the triangle can be determined using Heron's formula. In order for it to have a simpler form, a new value is used, which is called semi-perimeter. This is the sum of all the sides of our triangle, divided in half. After the semi-perimeter has been calculated, you can begin to determine the area using the formula:
S = sqrt(p(p-a)(p-b)(p-c)), where
sqrt - square root;
p - semi-perimeter value (p = (a+b+c)/2);
a, b, c - edges (sides) of the triangle.
But what if the triangle has an irregular shape? There are two possible ways here. The first of them is to try to divide such a figure into two right triangles, the sum of the areas of which is calculated separately, and then added. Or, if the angle between two sides and the size of these sides are known, then apply the formula:
S = 0.5 * ab * sinC, where
a,b - sides of the triangle;
c is the size of the angle between these sides.
The latter case is rare in practice, but nevertheless, everything is possible in life, so the above formula will not be superfluous. Good luck with your calculations!