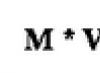What are the angles of a triangle? Triangle Angle Sum Theorem

Theorem on the sum of interior angles of a triangle

The sum of the angles of a triangle is 180°.

Proof:

• Given triangle ABC.
• Through vertex B we draw a straight line DK parallel to the base AC.
• \angle CBK= \angle C as internal crosswise lying with parallel DK and AC, and secant BC.
• \angle DBA = \angle A internal crosswise lying with DK \parallel AC and secant AB. Angle DBK is reversed and equal to
• \angle DBK = \angle DBA + \angle B + \angle CBK
• Since the unfolded angle is equal to 180 ^\circ , and \angle CBK = \angle C and \angle DBA = \angle A , we get 180 ^\circ = \angle A + \angle B + \angle C.

The theorem is proven

Corollaries from the theorem on the sum of angles of a triangle:

1. The sum of the acute angles of a right triangle is equal to 90°.
2. In an isosceles right triangle, each acute angle is equal to 45°.
3. In an equilateral triangle, each angle is equal 60°.
4. In any triangle, either all the angles are acute, or two angles are acute, and the third is obtuse or right.
5. An exterior angle of a triangle is equal to the sum of two interior angles that are not adjacent to it.

Triangle Exterior Angle Theorem

An exterior angle of a triangle is equal to the sum of the two remaining angles of the triangle that are not adjacent to this exterior angle

Proof:

• Given a triangle ABC, where BCD is the exterior angle.
• \angle BAC + \angle ABC +\angle BCA = 180^0
• From the equalities the angle \angle BCD + \angle BCA = 180^0
• We get \angle BCD = \angle BAC+\angle ABC.

A triangle is a polygon that has three sides (three angles). Most often, the sides are indicated by small letters corresponding to the capital letters that represent the opposite vertices. In this article we will get acquainted with the types of these geometric figures, the theorem that determines what the sum of the angles of a triangle equals.

Types by angle size

The following types of polygon with three vertices are distinguished:

• acute-angled, in which all the corners are sharp;
• rectangular, having one right angle, its generators are called legs, and the side that is located opposite the right angle is called the hypotenuse;
• obtuse when one ;
• isosceles, in which two sides are equal, and they are called lateral, and the third is the base of the triangle;
• equilateral, having all three equal sides.

Properties

There are basic properties that are characteristic of each type of triangle:

• Opposite the larger side there is always a larger angle, and vice versa;
• opposite equal sides there are equal angles, and vice versa;
• any triangle has two acute angles;
• an external angle is larger than any internal angle not adjacent to it;
• the sum of any two angles is always less than 180 degrees;
• the external angle is equal to the sum of the other two angles that do not intersect with it.

Triangle Angle Sum Theorem

The theorem states that if you add up all the angles of a given geometric figure, which is located on the Euclidean plane, then their sum will be 180 degrees. Let's try to prove this theorem.

Let us have an arbitrary triangle with vertices KMN.

Through vertex M we draw KN (this line is also called the Euclidean straight line). We mark point A on it so that points K and A are located on different sides of the straight line MH. We obtain equal angles AMN and KNM, which, like the internal ones, lie crosswise and are formed by the secant MN together with the straight lines KH and MA, which are parallel. It follows from this that the sum of the angles of the triangle located at the vertices M and H is equal to the size of the angle KMA. All three angles make up a sum that is equal to the sum of the angles KMA and MKN. Since these angles are internal one-sided relative to the parallel straight lines KN and MA with a secant KM, their sum is 180 degrees. The theorem has been proven.

Consequence

The following corollary follows from the theorem proved above: any triangle has two acute angles. To prove this, let us assume that this geometric figure has only one acute angle. It can also be assumed that none of the corners are acute. In this case, there must be at least two angles whose magnitude is equal to or greater than 90 degrees. But then the sum of the angles will be greater than 180 degrees. But this cannot happen, since according to the theorem, the sum of the angles of a triangle is equal to 180° - no more and no less. This is what needed to be proven.

Property of external angles

What is the sum of the exterior angles of a triangle? The answer to this question can be obtained using one of two methods. The first is that it is necessary to find the sum of the angles, which are taken one at each vertex, that is, three angles. The second implies that you need to find the sum of all six vertex angles. First, let's look at the first option. So, the triangle contains six external angles - two at each vertex.

Each pair has equal angles because they are vertical:

∟1 = ∟4, ∟2 = ∟5, ∟3 = ∟6.

In addition, it is known that the external angle of a triangle is equal to the sum of two internal ones that do not intersect with it. Hence,

∟1 = ∟A + ∟C, ∟2 = ∟A + ∟B, ∟3 = ∟B + ∟C.

From this it turns out that the sum of the external angles, which are taken one at each vertex, will be equal to:

∟1 + ∟2 + ∟3 = ∟A + ∟C + ∟A + ∟B + ∟B + ∟C = 2 x (∟A + ∟B + ∟C).

Taking into account the fact that the sum of the angles is equal to 180 degrees, we can say that ∟A + ∟B + ∟C = 180°. This means that ∟1 + ∟2 + ∟3 = 2 x 180° = 360°. If the second option is used, then the sum of the six angles will be, accordingly, twice as large. That is, the sum of the external angles of the triangle will be:

∟1 + ∟2 + ∟3 + ∟4 + ∟5 + ∟6 = 2 x (∟1 + ∟2 + ∟2) = 720°.

Right triangle

What is the sum of the acute angles of a right triangle? The answer to this question, again, follows from the theorem, which states that the angles in a triangle add up to 180 degrees. And our statement (property) sounds like this: in a right triangle, the acute angles add up to 90 degrees. Let's prove its veracity.

Let us be given a triangle KMN, in which ∟Н = 90°. It is necessary to prove that ∟К + ∟М = 90°.

So, according to the theorem on the sum of angles ∟К + ∟М + ∟Н = 180°. Our condition says that ∟Н = 90°. So it turns out, ∟К + ∟М + 90° = 180°. That is, ∟К + ∟М = 180° - 90° = 90°. This is exactly what we needed to prove.

In addition to the properties of a right triangle described above, you can add the following:

• angles that lie opposite the legs are acute;
• the hypotenuse is triangular larger than any of the legs;
• the sum of the legs is greater than the hypotenuse;
• The leg of the triangle, which lies opposite the angle of 30 degrees, is half the size of the hypotenuse, that is, equal to half of it.

As another property of this geometric figure, we can highlight the Pythagorean theorem. She states that in a triangle with an angle of 90 degrees (rectangular), the sum of the squares of the legs is equal to the square of the hypotenuse.

Sum of angles of an isosceles triangle

Earlier we said that an isosceles polygon with three vertices and containing two equal sides is called. This property of this geometric figure is known: the angles at its base are equal. Let's prove it.

Let's take the triangle KMN, which is isosceles, KN ​​is its base.

We are required to prove that ∟К = ∟Н. So, let's say that MA is the bisector of our triangle KMN. The triangle MKA, taking into account the first sign of equality, is equal to the triangle MNA. Namely, by condition it is given that KM = NM, MA is the common side, ∟1 = ∟2, since MA is a bisector. Using the fact that these two triangles are equal, we can state that ∟К = ∟Н. This means the theorem is proven.

But we are interested in what is the sum of the angles of a triangle (isosceles). Since in this respect it does not have its own peculiarities, we will build on the theorem discussed earlier. That is, we can say that ∟К + ∟М + ∟Н = 180°, or 2 x ∟К + ∟М = 180° (since ∟К = ∟Н). We will not prove this property, since the theorem on the sum of the angles of a triangle itself was proven earlier.

In addition to the properties discussed about the angles of a triangle, the following important statements also apply:

• at which it was lowered onto the base, is at the same time the median, the bisector of the angle that is between equal sides, as well as its base;
• the medians (bisectors, heights) that are drawn to the lateral sides of such a geometric figure are equal.

Equilateral triangle

It is also called regular, this is the triangle in which all sides are equal. And therefore the angles are also equal. Each one is 60 degrees. Let's prove this property.

Let's say that we have a triangle KMN. We know that KM = NM = KN. This means that, according to the property of the angles located at the base in an isosceles triangle, ∟К = ∟М = ∟Н. Since, according to the theorem, the sum of the angles of a triangle is ∟К + ∟М + ∟Н = 180°, then 3 x ∟К = 180° or ∟К = 60°, ∟М = 60°, ∟Н = 60°. Thus, the statement is proven.

As can be seen from the above proof based on the theorem, the sum of the angles, like the sum of the angles of any other triangle, is 180 degrees. There is no need to prove this theorem again.

There are also such properties characteristic of an equilateral triangle:

• the median, bisector, height in such a geometric figure coincide, and their length is calculated as (a x √3): 2;
• if we describe a circle around a given polygon, then its radius will be equal to (a x √3): 3;
• if you inscribe a circle in an equilateral triangle, then its radius will be (a x √3): 6;
• The area of ​​this geometric figure is calculated by the formula: (a2 x √3) : 4.

Obtuse triangle

By definition, one of its angles is between 90 and 180 degrees. But given that the other two angles of this geometric figure are acute, we can conclude that they do not exceed 90 degrees. Therefore, the triangle angle sum theorem works in calculating the sum of angles in an obtuse triangle. It turns out that we can safely say, based on the above-mentioned theorem, that the sum of the angles of an obtuse triangle is equal to 180 degrees. Again, this theorem does not need to be proven again.

Preliminary information

First, let's look directly at the concept of a triangle.

Definition 1

We will call a triangle a geometric figure that is made up of three points connected to each other by segments (Fig. 1).

Definition 2

Within the framework of Definition 1, we will call the points the vertices of the triangle.

Definition 3

Within the framework of Definition 1, the segments will be called sides of the triangle.

Obviously, any triangle will have 3 vertices, as well as three sides.

Theorem on the sum of angles in a triangle

Let us introduce and prove one of the main theorems related to triangles, namely the theorem on the sum of angles in a triangle.

Theorem 1

The sum of the angles in any arbitrary triangle is $180^\circ$.

Proof.

Consider the triangle $EGF$. Let us prove that the sum of the angles in this triangle is equal to $180^\circ$. Let's make an additional construction: draw the straight line $XY||EG$ (Fig. 2)

Since the lines $XY$ and $EG$ are parallel, then $∠E=∠XFE$ lie crosswise at the secant $FE$, and $∠G=∠YFG$ lie crosswise at the secant $FG$

Angle $XFY$ will be reversed and therefore equals $180^\circ$.

$∠XFY=∠XFE+∠F+∠YFG=180^\circ$

Hence

$∠E+∠F+∠G=180^\circ$

The theorem has been proven.

Triangle Exterior Angle Theorem

Another theorem on the sum of angles for a triangle can be considered the theorem on the external angle. First, let's introduce this concept.

Definition 4

We will call an external angle of a triangle an angle that will be adjacent to any angle of the triangle (Fig. 3).

Let us now consider the theorem directly.

Theorem 2

An exterior angle of a triangle is equal to the sum of two angles of the triangle that are not adjacent to it.

Proof.

Consider an arbitrary triangle $EFG$. Let it have an external angle of the triangle $FGQ$ (Fig. 3).

By Theorem 1, we will have that $∠E+∠F+∠G=180^\circ$, therefore,

$∠G=180^\circ-(∠E+∠F)$

Since the angle $FGQ$ is external, it is adjacent to the angle $∠G$, then

$∠FGQ=180^\circ-∠G=180^\circ-180^\circ+(∠E+∠F)=∠E+∠F$

The theorem has been proven.

Sample tasks

Example 1

Find all angles of a triangle if it is equilateral.

Since all the sides of an equilateral triangle are equal, we will have that all the angles in it are also equal to each other. Let us denote their degree measures by $α$.

Then, by Theorem 1 we get

$α+α+α=180^\circ$

Answer: all angles equal $60^\circ$.

Example 2

Find all angles of an isosceles triangle if one of its angles is equal to $100^\circ$.

Let us introduce the following notation for angles in an isosceles triangle:

Since we are not given in the condition exactly what angle $100^\circ$ is equal to, then two cases are possible:

An angle equal to $100^\circ$ is the angle at the base of the triangle.

Using the theorem on angles at the base of an isosceles triangle, we obtain

$∠2=∠3=100^\circ$

But then only their sum will be greater than $180^\circ$, which contradicts the conditions of Theorem 1. This means that this case does not occur.

An angle equal to $100^\circ$ is the angle between equal sides, that is

Theorem. The sum of the interior angles of a triangle is equal to two right angles.

Let's take some triangle ABC (Fig. 208). Let us denote its interior angles by numbers 1, 2 and 3. Let us prove that

∠1 + ∠2 + ∠3 = 180°.

Let us draw through some vertex of the triangle, for example B, a straight line MN parallel to AC.

At vertex B we got three angles: ∠4, ∠2 and ∠5. Their sum is a straight angle, therefore it is equal to 180°:

∠4 + ∠2 + ∠5 = 180°.

But ∠4 = ∠1 are internal crosswise angles with parallel lines MN and AC and secant AB.

∠5 = ∠3 - these are internal crosswise angles with parallel lines MN and AC and secant BC.

This means that ∠4 and ∠5 can be replaced by their equals ∠1 and ∠3.

Therefore, ∠1 + ∠2 + ∠3 = 180°. The theorem has been proven.

2. Property of the external angle of a triangle.

Theorem. An exterior angle of a triangle is equal to the sum of two interior angles that are not adjacent to it.




In fact, in triangle ABC (Fig. 209) ∠1 + ∠2 = 180° - ∠3, but also ∠ВСD, the external angle of this triangle, not adjacent to ∠1 and ∠2, is also equal to 180° - ∠3 .

Thus:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

Therefore, ∠1 + ∠2= ∠BCD.

The derived property of the exterior angle of a triangle clarifies the content of the previously proven theorem on the exterior angle of a triangle, which stated only that the exterior angle of a triangle is greater than each interior angle of a triangle not adjacent to it; now it is established that the external angle is equal to the sum of both internal angles not adjacent to it.

3. Property of a right triangle with an angle of 30°.

Theorem. A leg of a right triangle lying opposite an angle of 30° is equal to half the hypotenuse.


Let angle B in the right triangle ACB be equal to 30° (Fig. 210). Then its other acute angle will be equal to 60°.



Let us prove that leg AC is equal to half the hypotenuse AB. Let's extend the leg AC beyond the vertex of the right angle C and set aside a segment CM equal to the segment AC. Let's connect point M to point B. The resulting triangle ВСМ is equal to triangle ACB. We see that each angle of triangle ABM is equal to 60°, therefore this triangle is an equilateral triangle.

Leg AC is equal to half AM, and since AM is equal to AB, leg AC will be equal to half the hypotenuse AB.