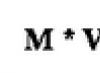Hypothesis: we believe that the perfection of the pyramid's shape is due to the mathematical laws inherent in its shape.

Target: Having studied the pyramid as a geometric body, explain the perfection of its form.

Tasks:

1. Give a mathematical definition of a pyramid.

2. Study the pyramid as a geometric body.

3. Understand what mathematical knowledge the Egyptians incorporated into their pyramids.

Private questions:

1. What is a pyramid as a geometric body?

2. How can the unique shape of the pyramid be explained from a mathematical point of view?

3. What explains the geometric wonders of the pyramid?

4. What explains the perfection of the pyramid shape?

Definition of a pyramid.

PYRAMID (from Greek pyramis, gen. pyramidos) - a polyhedron whose base is a polygon, and the remaining faces are triangles having a common vertex (drawing). Based on the number of corners of the base, pyramids are classified as triangular, quadrangular, etc.

PYRAMID - a monumental structure that has the geometric shape of a pyramid (sometimes also stepped or tower-shaped). Pyramids are the name given to the giant tombs of the ancient Egyptian pharaohs of the 3rd-2nd millennium BC. e., as well as ancient American temple pedestals (in Mexico, Guatemala, Honduras, Peru), associated with cosmological cults.

It is possible that the Greek word “pyramid” comes from the Egyptian expression per-em-us, i.e., from a term meaning the height of the pyramid. The outstanding Russian Egyptologist V. Struve believed that the Greek “puram...j” comes from the ancient Egyptian “p"-mr”.

From the history. Having studied the material in the textbook “Geometry” by the authors of Atanasyan. Butuzov and others, we learned that: A polyhedron composed of a n-gon A1A2A3 ... An and n triangles PA1A2, PA2A3, ..., PAnA1 is called a pyramid. Polygon A1A2A3...An is the base of the pyramid, and triangles PA1A2, PA2A3,..., PAnA1 are the side faces of the pyramid, P is the top of the pyramid, segments PA1, PA2,..., PAn are the side edges.

However, this definition of a pyramid did not always exist. For example, the ancient Greek mathematician, the author of theoretical treatises on mathematics that has come down to us, Euclid, defines a pyramid as a solid figure limited by planes that converge from one plane to one point.

But this definition was criticized already in ancient times. So Heron proposed the following definition of a pyramid: “It is a figure bounded by triangles converging at one point and the base of which is a polygon.”

Our group, having compared these definitions, came to the conclusion that they do not have a clear formulation of the concept of “foundation”.

We examined these definitions and found the definition of Adrien Marie Legendre, who in 1794 in his work “Elements of Geometry” defines a pyramid as follows: “A pyramid is a solid figure formed by triangles converging at one point and ending on different sides of a flat base.”

It seems to us that the last definition gives a clear idea of ​​the pyramid, since it talks about the fact that the base is flat. Another definition of a pyramid appeared in a 19th-century textbook: “a pyramid is a solid angle intersected by a plane.”

Pyramid as a geometric body.

That. A pyramid is a polyhedron, one of whose faces (base) is a polygon, the remaining faces (sides) are triangles that have one common vertex (the vertex of the pyramid).

The perpendicular drawn from the top of the pyramid to the plane of the base is called heighth pyramids.

In addition to the arbitrary pyramid, there are correct pyramid at the base of which is a regular polygon and truncated pyramid.

In the figure there is a pyramid PABCD, ABCD is its base, PO is its height.

Total surface area of a pyramid is the sum of the areas of all its faces.

Sfull = Sside + Smain, Where Side– the sum of the areas of the side faces.

Volume of the pyramid is found by the formula:

V=1/3Sbas. h, where Sbas. - base area, h- height.

The area of ​​the lateral face of a regular pyramid is expressed as follows: Sside. =1/2P h, where P is the perimeter of the base, h- height of the side face (apothem of a regular pyramid). If the pyramid is intersected by the plane A’B’C’D’, parallel to the base, then:

1) the side ribs and height are divided by this plane into proportional parts;

2) in cross-section a polygon A’B’C’D’ is obtained, similar to the base;

https://pandia.ru/text/78/390/images/image017_1.png" width="287" height="151">

Bases of a truncated pyramid– similar polygons ABCD and A`B`C`D`, side faces are trapezoids.

Height truncated pyramid - the distance between the bases.

Truncated volume pyramid is found by the formula:

V=1/3 h(S + https://pandia.ru/text/78/390/images/image019_2.png" align="left" width="91" height="96"> The lateral surface area of ​​a regular truncated pyramid is expressed as follows: Sside. = ½(P+P') h, where P and P’ are the perimeters of the bases, h- height of the side face (apothem of a regular truncated pier

Sections of a pyramid.

Sections of a pyramid by planes passing through its apex are triangles.

A section passing through two non-adjacent lateral edges of a pyramid is called diagonal section.

If the section passes through a point on the side edge and the side of the base, then its trace to the plane of the base of the pyramid will be this side.

A section passing through a point lying on the face of the pyramid and a given section trace on the base plane, then the construction should be carried out as follows:

· find the point of intersection of the plane of a given face and the trace of the section of the pyramid and designate it;

· construct a straight line passing through a given point and the resulting intersection point;

· repeat these steps for the next faces.

, which corresponds to the ratio of the legs of a right triangle 4:3. This ratio of the legs corresponds to the well-known right triangle with sides 3:4:5, which is called the “perfect”, “sacred” or “Egyptian” triangle. According to historians, the “Egyptian” triangle was given a magical meaning. Plutarch wrote that the Egyptians compared the nature of the universe to a “sacred” triangle; they symbolically likened the vertical leg to the husband, the base to the wife, and the hypotenuse to that which is born from both.

For a triangle 3:4:5, the equality is true: 32 + 42 = 52, which expresses the Pythagorean theorem. Was it not this theorem that the Egyptian priests wanted to perpetuate when they built a pyramid based on the triangle 3:4:5? It is difficult to find a more successful example to illustrate the Pythagorean theorem, which was known to the Egyptians long before its discovery by Pythagoras.

Thus, the brilliant creators of the Egyptian pyramids sought to amaze distant descendants with the depth of their knowledge, and they achieved this by choosing the “golden” right triangle as the “main geometric idea” for the Cheops pyramid, and the “sacred” or “Egyptian” for the Khafre pyramid. triangle.

Very often in their research, scientists use the properties of pyramids with Golden Ratio proportions.

The mathematical encyclopedic dictionary gives the following definition of the Golden Section - this is a harmonic division, division in extreme and mean ratios - dividing the segment AB into two parts in such a way that its larger part AC is the average proportional between the entire segment AB and its smaller part NE.

Algebraic determination of the Golden section of a segment AB = a reduces to solving the equation a: x = x: (a – x), from which x is approximately equal to 0.62a. The ratio x can be expressed as fractions 2/3, 3/5, 5/8, 8/13, 13/21...= 0.618, where 2, 3, 5, 8, 13, 21 are Fibonacci numbers.

The geometric construction of the Golden Section of the segment AB is carried out as follows: at point B, a perpendicular to AB is restored, the segment BE = 1/2 AB is laid out on it, A and E are connected, DE = BE is laid off and, finally, AC = AD, then the equality AB is satisfied: CB = 2:3.

The golden ratio is often used in works of art, architecture, and is found in nature. Vivid examples are the sculpture of Apollo Belvedere and the Parthenon. During the construction of the Parthenon, the ratio of the height of the building to its length was used and this ratio is 0.618. Objects around us also provide examples of the Golden Ratio, for example, the bindings of many books have a width-to-length ratio close to 0.618. Considering the arrangement of leaves on the common stem of plants, you can notice that between every two pairs of leaves the third is located at the Golden Ratio (slides). Each of us “carries” the Golden Ratio with us “in our hands” - this is the ratio of the phalanges of the fingers.

Thanks to the discovery of several mathematical papyri, Egyptologists have learned something about the ancient Egyptian systems of calculation and measurement. The tasks contained in them were solved by scribes. One of the most famous is the Rhind Mathematical Papyrus. By studying these problems, Egyptologists learned how the ancient Egyptians dealt with the various quantities that arose when calculating measures of weight, length, and volume, which often involved fractions, as well as how they handled angles.

The ancient Egyptians used a method of calculating angles based on the ratio of the height to the base of a right triangle. They expressed any angle in the language of a gradient. The slope gradient was expressed as a whole number ratio called "seced". In Mathematics in the Age of the Pharaohs, Richard Pillins explains: “The seked of a regular pyramid is the inclination of any of the four triangular faces to the plane of the base, measured by the nth number of horizontal units per vertical unit of rise. Thus, this unit of measurement is equivalent to our modern cotangent of the angle of inclination. Therefore, the Egyptian word "seced" is related to our modern word "gradient."

The numerical key to the pyramids lies in the ratio of their height to the base. In practical terms, this is the easiest way to make the templates necessary to constantly check the correct angle of inclination throughout the construction of the pyramid.

Egyptologists would be happy to convince us that each pharaoh longed to express his individuality, hence the differences in the angles of inclination for each pyramid. But there could be another reason. Perhaps they all wanted to embody different symbolic associations, hidden in different proportions. However, the angle of Khafre's pyramid (based on the triangle (3:4:5) appears in the three problems presented by the pyramids in the Rhind Mathematical Papyrus). So this attitude was well known to the ancient Egyptians.

To be fair to Egyptologists who claim that the ancient Egyptians were not aware of the 3:4:5 triangle, the length of the hypotenuse 5 was never mentioned. But mathematical problems involving pyramids are always solved on the basis of the seceda angle - the ratio of the height to the base. Since the length of the hypotenuse was never mentioned, it was concluded that the Egyptians never calculated the length of the third side.

The height-to-base ratios used in the Giza pyramids were undoubtedly known to the ancient Egyptians. It is possible that these relationships for each pyramid were chosen arbitrarily. However, this contradicts the importance attached to number symbolism in all types of Egyptian fine art. It is very likely that such relationships were significant because they expressed specific religious ideas. In other words, the entire Giza complex was subordinated to a coherent design designed to reflect a certain divine theme. This would explain why the designers chose different angles for the three pyramids.

In The Orion Mystery, Bauval and Gilbert presented compelling evidence linking the Giza pyramids to the constellation Orion, particularly the stars of Orion's Belt. The same constellation is present in the myth of Isis and Osiris, and there is reason to view each pyramid as a representation of one of the three main deities - Osiris, Isis and Horus.

"GEOMETRICAL" MIRACLES.

Among the grandiose pyramids of Egypt, it occupies a special place Great Pyramid of Pharaoh Cheops (Khufu). Before we begin to analyze the shape and size of the Cheops pyramid, we should remember what system of measures the Egyptians used. The Egyptians had three units of length: a "cubit" (466 mm), which was equal to seven "palms" (66.5 mm), which, in turn, was equal to four "fingers" (16.6 mm).

Let us analyze the dimensions of the Cheops pyramid (Fig. 2), following the arguments given in the wonderful book of the Ukrainian scientist Nikolai Vasyutinsky “The Golden Proportion” (1990).

Most researchers agree that the length of the side of the base of the pyramid, for example, GF equal to L= 233.16 m. This value corresponds almost exactly to 500 “elbows”. Full compliance with 500 “elbows” will occur if the length of the “elbow” is considered equal to 0.4663 m.

Height of the pyramid ( H) is estimated by researchers variously from 146.6 to 148.2 m. And depending on the accepted height of the pyramid, all the relationships of its geometric elements change. What is the reason for the differences in estimates of the height of the pyramid? The fact is that, strictly speaking, the Cheops pyramid is truncated. Its upper platform today measures approximately 10 ´ 10 m, but a century ago it was 6 ´ 6 m. Obviously, the top of the pyramid was dismantled, and it does not correspond to the original one.

When assessing the height of the pyramid, it is necessary to take into account such a physical factor as the “draft” of the structure. Over a long period of time, under the influence of colossal pressure (reaching 500 tons per 1 m2 of the lower surface), the height of the pyramid decreased compared to its original height.

What was the original height of the pyramid? This height can be recreated by finding the basic "geometric idea" of the pyramid.

Figure 2.

In 1837, the English Colonel G. Wise measured the angle of inclination of the faces of the pyramid: it turned out to be equal a= 51°51". This value is still recognized by most researchers today. The specified angle value corresponds to the tangent (tg a), equal to 1.27306. This value corresponds to the ratio of the height of the pyramid AC to half its base C.B.(Fig.2), that is A.C. / C.B. = H / (L / 2) = 2H / L.

And here the researchers were in for a big surprise!.png" width="25" height="24">= 1.272. Comparing this value with the tg value a= 1.27306, we see that these values ​​are very close to each other. If we take the angle a= 51°50", that is, reduce it by just one arc minute, then the value a will become equal to 1.272, that is, it will coincide with the value. It should be noted that in 1840 G. Wise repeated his measurements and clarified that the value of the angle a=51°50".

These measurements led the researchers to the following very interesting hypothesis: the triangle ACB of the Cheops pyramid was based on the relation AC / C.B. = = 1,272!

Consider now the right triangle ABC, in which the ratio of the legs A.C. / C.B.= (Fig. 2). If now the lengths of the sides of the rectangle ABC designate by x, y, z, and also take into account that the ratio y/x= , then in accordance with the Pythagorean theorem, the length z can be calculated using the formula:

If we accept x = 1, y= https://pandia.ru/text/78/390/images/image027_1.png" width="143" height="27">

Figure 3."Golden" right triangle.

A right triangle in which the sides are related as t:golden" right triangle.

Then, if we take as a basis the hypothesis that the main “geometric idea” of the Cheops pyramid is a “golden” right triangle, then from here we can easily calculate the “design” height of the Cheops pyramid. It is equal to:

H = (L/2) ´ = 148.28 m.

Let us now derive some other relations for the Cheops pyramid, which follow from the “golden” hypothesis. In particular, we will find the ratio of the outer area of ​​the pyramid to the area of ​​its base. To do this, we take the length of the leg C.B. per unit, that is: C.B.= 1. But then the length of the side of the base of the pyramid GF= 2, and the area of ​​the base EFGH will be equal SEFGH = 4.

Let us now calculate the area of ​​the side face of the Cheops pyramid SD. Because the height AB triangle AEF equal to t, then the area of ​​the side face will be equal to SD = t. Then the total area of ​​all four lateral faces of the pyramid will be equal to 4 t, and the ratio of the total outer area of ​​the pyramid to the area of ​​the base will be equal to the golden ratio! That's what it is - the main geometric mystery of the Cheops pyramid!

The group of “geometric miracles” of the Cheops pyramid includes real and far-fetched properties of the relationships between various dimensions in the pyramid.

As a rule, they are obtained in search of certain “constants”, in particular, the number “pi” (Ludolfo’s number), equal to 3.14159...; the base of natural logarithms "e" (Neperovo number), equal to 2.71828...; the number "F", the number of the "golden section", equal to, for example, 0.618... etc.

You can name, for example: 1) Property of Herodotus: (Height)2 = 0.5 art. basic x Apothem; 2) Property of V. Price: Height: 0.5 art. base = Square root of "F"; 3) Property of M. Eist: Perimeter of the base: 2 Height = "Pi"; in a different interpretation - 2 tbsp. basic : Height = "Pi"; 4) Property of G. Edge: Radius of the inscribed circle: 0.5 art. basic = "F"; 5) Property of K. Kleppisch: (Art. main.)2: 2(Art. main. x Apothem) = (Art. main. W. Apothema) = 2(Art. main. x Apothem) : ((2 art. main X Apothem) + (v. main)2). Etc. You can come up with many such properties, especially if you connect two adjacent pyramids. For example, as “Properties of A. Arefyev” it can be mentioned that the difference in the volumes of the pyramid of Cheops and the pyramid of Khafre is equal to twice the volume of the pyramid of Mikerin...

Many interesting points, in particular about the construction of pyramids according to the “golden ratio”, are set out in the books by D. Hambidge “Dynamic symmetry in architecture” and M. Gick “Aesthetics of proportion in nature and art”. Let us recall that the “golden ratio” is the division of a segment in such a ratio that part A is as many times greater than part B, how many times A is smaller than the entire segment A + B. The ratio A/B is equal to the number “F” == 1.618. .. The use of the “golden ratio” is indicated not only in individual pyramids, but also in the entire complex of pyramids at Giza.

The most curious thing, however, is that one and the same Cheops pyramid simply “cannot” contain so many wonderful properties. Taking a certain property one by one, it can be “fitted”, but all of them do not fit at once - they do not coincide, they contradict each other. Therefore, if, for example, when checking all properties, we initially take the same side of the base of the pyramid (233 m), then the heights of pyramids with different properties will also be different. In other words, there is a certain “family” of pyramids that are externally similar to Cheops, but have different properties. Note that there is nothing particularly miraculous in the “geometric” properties - much arises purely automatically, from the properties of the figure itself. A “miracle” should only be considered something that was clearly impossible for the ancient Egyptians. This, in particular, includes “cosmic” miracles, in which the measurements of the Cheops pyramid or the pyramid complex at Giza are compared with some astronomical measurements and “even” numbers are indicated: a million times less, a billion times less, and so on. Let's consider some "cosmic" relationships.

One of the statements is: “if you divide the side of the base of the pyramid by the exact length of the year, you get exactly 10 millionths of the earth’s axis.” Calculate: divide 233 by 365, we get 0.638. The radius of the Earth is 6378 km.

Another statement is actually the opposite of the previous one. F. Noetling pointed out that if we use the “Egyptian cubit” he himself invented, then the side of the pyramid will correspond to “the most accurate duration of the solar year, expressed to the nearest one billionth of a day” - 365.540.903.777.

P. Smith's statement: "The height of the pyramid is exactly one billionth of the distance from the Earth to the Sun." Although the height usually taken is 146.6 m, Smith took it as 148.2 m. According to modern radar measurements, the semi-major axis of the earth's orbit is 149,597,870 + 1.6 km. This is the average distance from the Earth to the Sun, but at perihelion it is 5,000,000 kilometers less than at aphelion.

One last interesting statement:

“How can we explain that the masses of the pyramids of Cheops, Khafre and Mykerinus relate to each other, like the masses of the planets Earth, Venus, Mars?” Let's calculate. The masses of the three pyramids are: Khafre - 0.835; Cheops - 1,000; Mikerin - 0.0915. The ratios of the masses of the three planets: Venus - 0.815; Earth - 1,000; Mars - 0.108.

So, despite skepticism, we note the well-known harmony of the construction of statements: 1) the height of the pyramid, like a line “going into space”, corresponds to the distance from the Earth to the Sun; 2) the side of the base of the pyramid, closest “to the substrate,” that is, to the Earth, is responsible for the earth’s radius and earth’s circulation; 3) the volumes of the pyramid (read - masses) correspond to the ratio of the masses of the planets closest to the Earth. A similar “cipher” can be traced, for example, in the bee language analyzed by Karl von Frisch. However, we will refrain from commenting on this matter for now.

PYRAMID SHAPE

The famous tetrahedral shape of the pyramids did not arise immediately. The Scythians made burials in the form of earthen hills - mounds. The Egyptians built "hills" of stone - pyramids. This first happened after the unification of Upper and Lower Egypt, in the 28th century BC, when the founder of the Third Dynasty, Pharaoh Djoser (Zoser), was faced with the task of strengthening the unity of the country.

And here, according to historians, the “new concept of deification” of the king played an important role in strengthening central power. Although the royal burials were distinguished by greater splendor, they, in principle, did not differ from the tombs of court nobles; they were the same structures - mastabas. Above the chamber with the sarcophagus containing the mummy, a rectangular hill of small stones was poured, where a small building made of large stone blocks - a “mastaba” (in Arabic - “bench”) was then placed. Pharaoh Djoser erected the first pyramid on the site of the mastaba of his predecessor, Sanakht. It was stepped and was a visible transitional stage from one architectural form to another, from a mastaba to a pyramid.

In this way, the sage and architect Imhotep, who was later considered a wizard and identified by the Greeks with the god Asclepius, “raised” the pharaoh. It was as if six mastabas were erected in a row. Moreover, the first pyramid occupied an area of ​​1125 x 115 meters, with an estimated height of 66 meters (according to Egyptian standards - 1000 “palms”). At first, the architect planned to build a mastaba, but not oblong, but square in plan. Later it was expanded, but since the extension was made lower, it seemed like there were two steps.

This situation did not satisfy the architect, and on the upper platform of the huge flat mastaba, Imhotep placed three more, gradually decreasing towards the top. The tomb was located under the pyramid.

Several more step pyramids are known, but later the builders moved on to building tetrahedral pyramids that are more familiar to us. Why, however, not triangular or, say, octagonal? An indirect answer is given by the fact that almost all pyramids are perfectly oriented along the four cardinal directions, and therefore have four sides. In addition, the pyramid was a “house”, the shell of a quadrangular burial chamber.

But what determined the angle of inclination of the faces? In the book “The Principle of Proportions” an entire chapter is devoted to this: “What could have determined the angles of inclination of the pyramids.” In particular, it is indicated that “the image to which the great pyramids of the Old Kingdom gravitate is a triangle with a right angle at the apex.

In space it is a semi-octahedron: a pyramid in which the edges and sides of the base are equal, the edges are equilateral triangles." Certain considerations are given on this subject in the books of Hambidge, Gick and others.

What is the advantage of the semi-octahedron angle? According to descriptions by archaeologists and historians, some pyramids collapsed under their own weight. What was needed was a “durability angle,” an angle that was the most energetically reliable. Purely empirically, this angle can be taken from the vertex angle in a pile of crumbling dry sand. But to get accurate data, you need to use a model. Taking four firmly fixed balls, you need to place a fifth one on them and measure the angles of inclination. However, you can make a mistake here, so a theoretical calculation helps: you should connect the centers of the balls with lines (mentally). The base will be a square with a side equal to twice the radius. The square will be just the base of the pyramid, the length of the edges of which will also be equal to twice the radius.

Thus, a close packing of balls like 1:4 will give us a regular semi-octahedron.

However, why do many pyramids, gravitating towards a similar shape, nevertheless not retain it? The pyramids are probably aging. Contrary to the famous saying:

“Everything in the world is afraid of time, and time is afraid of pyramids,” the buildings of the pyramids must age, not only processes of external weathering can and should occur in them, but also processes of internal “shrinkage,” which may cause the pyramids to become lower. Shrinkage is also possible because, as revealed by the work of D. Davidovits, the ancient Egyptians used the technology of making blocks from lime chips, in other words, from “concrete”. It is precisely similar processes that could explain the reason for the destruction of the Medum Pyramid, located 50 km south of Cairo. It is 4600 years old, the dimensions of the base are 146 x 146 m, the height is 118 m. “Why is it so disfigured?” asks V. Zamarovsky. “The usual references to the destructive effects of time and the “use of stone for other buildings” are not suitable here.

After all, most of its blocks and facing slabs have remained in place to this day, in ruins at its foot." As we will see, a number of provisions even make us think that the famous pyramid of Cheops also "shrivelled." In any case, in all ancient images the pyramids are pointed ...

The shape of the pyramids could also have been generated by imitation: some natural samples, “miracle perfection,” say, some crystals in the form of an octahedron.

Similar crystals could be diamond and gold crystals. A large number of “overlapping” features are typical for such concepts as Pharaoh, Sun, Gold, Diamond. Everywhere - noble, brilliant (brilliant), great, impeccable, and so on. The similarities are not accidental.

The solar cult, as is known, formed an important part of the religion of Ancient Egypt. “No matter how we translate the name of the greatest of the pyramids,” notes one of the modern manuals, “The Sky of Khufu” or “The Skyward Khufu,” it meant that the king is the sun.” If Khufu, in the brilliance of his power, imagined himself to be the second sun, then his son Djedef-Ra became the first of the Egyptian kings to call himself the “son of Ra,” that is, the son of the Sun. The sun, in almost all nations, was symbolized by the “solar metal”, gold. “A large disk of bright gold” - that’s what the Egyptians called our daylight. The Egyptians knew gold perfectly, they knew its native forms, where gold crystals can appear in the form of octahedrons.

The “sun stone”—diamond—is also interesting here as a “sample of forms.” The name of the diamond came precisely from the Arab world, “almas” - the hardest, most hard, indestructible. The ancient Egyptians knew diamond and its properties quite well. According to some authors, they even used bronze tubes with diamond cutters for drilling.

Nowadays the main supplier of diamonds is South Africa, but Western Africa is also rich in diamonds. The territory of the Republic of Mali is even called the “Diamond Land”. Meanwhile, it is on the territory of Mali that the Dogon live, with whom supporters of the paleo-visit hypothesis pin many hopes (see below). Diamonds could not have been the reason for the contacts of the ancient Egyptians with this region. However, one way or another, it is possible that precisely by copying the octahedrons of diamond and gold crystals, the ancient Egyptians thereby deified the pharaohs, “indestructible” like diamond and “brilliant” like gold, the sons of the Sun, comparable only to the most wonderful creations of nature.

Conclusion:

Having studied the pyramid as a geometric body, becoming acquainted with its elements and properties, we were convinced of the validity of the opinion about the beauty of the shape of the pyramid.

As a result of our research, we came to the conclusion that the Egyptians, having collected the most valuable mathematical knowledge, embodied it in a pyramid. Therefore, the pyramid is truly the most perfect creation of nature and man.

BIBLIOGRAPHY

"Geometry: Textbook. for 7 – 9 grades. general education institutions\, etc. - 9th ed. - M.: Education, 1999

History of mathematics in school, M: “Prosveshchenie”, 1982.

Geometry 10-11 grades, M: “Enlightenment”, 2000

Peter Tompkins “Secrets of the Great Pyramid of Cheops”, M: “Tsentropoligraf”, 2005.

Internet resources

http://veka-i-mig. *****/

http://tambov. *****/vjpusk/vjp025/rabot/33/index2.htm

http://www. *****/enc/54373.html

Students encounter the concept of a pyramid long before studying geometry. The fault lies with the famous great Egyptian wonders of the world. Therefore, when starting to study this wonderful polyhedron, most students already clearly imagine it. All the above-mentioned attractions have the correct shape. What's happened regular pyramid, and what properties it has will be discussed further.

In contact with

Definition

There are quite a lot of definitions of a pyramid. Since ancient times, it has been very popular.

For example, Euclid defined it as a bodily figure consisting of planes that, starting from one, converge at a certain point.

Heron provided a more precise formulation. He insisted that this was the figure that has a base and planes in the form of triangles, converging at one point.

Based on the modern interpretation, the pyramid is represented as a spatial polyhedron, consisting of a certain k-gon and k flat triangular figures, having one common point.

Let's look at it in more detail, what elements does it consist of:

• The k-gon is considered the basis of the figure;
• 3-gonal shapes protrude as the edges of the side part;
• the upper part from which the side elements originate is called the apex;
• all segments connecting a vertex are called edges;
• if a straight line is lowered from the vertex to the plane of the figure at an angle of 90 degrees, then its part contained in the internal space is the height of the pyramid;
• in any lateral element, a perpendicular, called an apothem, can be drawn to the side of our polyhedron.

The number of edges is calculated using the formula 2*k, where k is the number of sides of the k-gon. How many faces a polyhedron such as a pyramid has can be determined using the expression k+1.

Important! A pyramid of regular shape is a stereometric figure whose base plane is a k-gon with equal sides.

Basic properties

Correct pyramid has many properties, which are unique to her. Let's list them:

1. The basis is a figure of the correct shape.
2. The edges of the pyramid that limit the side elements have equal numerical values.
3. The side elements are isosceles triangles.
4. The base of the height of the figure falls at the center of the polygon, while it is simultaneously the central point of the inscribed and circumscribed.
5. All side ribs are inclined to the plane of the base at the same angle.
6. All side surfaces have the same angle of inclination relative to the base.

Thanks to all of the listed properties, performing element calculations is much simpler. Based on the above properties, we pay attention to two signs:

1. In the case when the polygon fits into a circle, the side faces will have equal angles with the base.
2. When describing a circle around a polygon, all edges of the pyramid emanating from the vertex will have equal lengths and equal angles with the base.

The basis is a square

Regular quadrangular pyramid - a polyhedron whose base is a square.

It has four side faces, which are isosceles in appearance.

A square is depicted on a plane, but is based on all the properties of a regular quadrilateral.

For example, if it is necessary to relate the side of a square with its diagonal, then use the following formula: the diagonal is equal to the product of the side of the square and the square root of two.

It is based on a regular triangle

A regular triangular pyramid is a polyhedron whose base is a regular 3-gon.

If the base is a regular triangle and the side edges are equal to the edges of the base, then such a figure called a tetrahedron.

All faces of a tetrahedron are equilateral 3-gons. In this case, you need to know some points and not waste time on them when calculating:

• the angle of inclination of the ribs to any base is 60 degrees;
• the size of all internal faces is also 60 degrees;
• any face can act as a base;
• , drawn inside the figure, these are equal elements.

Sections of a polyhedron

In any polyhedron there are several types of sections flat. Often in a school geometry course they work with two:

• axial;
• parallel to the basis.

An axial section is obtained by intersecting a polyhedron with a plane that passes through the vertex, side edges and axis. In this case, the axis is the height drawn from the vertex. The cutting plane is limited by the lines of intersection with all faces, resulting in a triangle.

Attention! In a regular pyramid, the axial section is an isosceles triangle.

If the cutting plane runs parallel to the base, then the result is the second option. In this case, we have a cross-sectional figure similar to the base.

For example, if there is a square at the base, then the section parallel to the base will also be a square, only of smaller dimensions.

When solving problems under this condition, they use signs and properties of similarity of figures, based on Thales' theorem. First of all, it is necessary to determine the similarity coefficient.

If the plane is drawn parallel to the base and it cuts off the upper part of the polyhedron, then a regular truncated pyramid is obtained in the lower part. Then the bases of a truncated polyhedron are said to be similar polygons. In this case, the side faces are isosceles trapezoids. The axial section is also isosceles.

In order to determine the height of a truncated polyhedron, it is necessary to draw the height in the axial section, that is, in the trapezoid.

Surface areas

The main geometric problems that have to be solved in a school geometry course are finding the surface area and volume of a pyramid.

There are two types of surface area values:

• area of ​​the side elements;
• area of ​​the entire surface.

From the name itself it is clear what we are talking about. The side surface includes only the side elements. It follows from this that to find it, you simply need to add up the areas of the lateral planes, that is, the areas of isosceles 3-gons. Let's try to derive the formula for the area of ​​the side elements:

1. The area of ​​an isosceles 3-gon is Str=1/2(aL), where a is the side of the base, L is the apothem.
2. The number of lateral planes depends on the type of k-gon at the base. For example, a regular quadrangular pyramid has four lateral planes. Therefore, it is necessary to add the areas of four figures Sside=1/2(aL)+1/2(aL)+1/2(aL)+1/2(aL)=1/2*4a*L. The expression is simplified in this way because the value is 4a = Rosn, where Rosn is the perimeter of the base. And the expression 1/2*Rosn is its semi-perimeter.
3. So, we conclude that the area of ​​the lateral elements of a regular pyramid is equal to the product of the semi-perimeter of the base and the apothem: Sside = Rosn * L.

The area of ​​the total surface of the pyramid consists of the sum of the areas of the side planes and the base: Sp.p. = Sside + Sbas.

As for the area of ​​the base, here the formula is used according to the type of polygon.

Volume of a regular pyramid equal to the product of the area of ​​the base plane and the height divided by three: V=1/3*Sbas*H, where H is the height of the polyhedron.

What is a regular pyramid in geometry

Properties of a regular quadrangular pyramid

Pyramid. Truncated pyramid

Pyramid is a polyhedron, one of whose faces is a polygon ( base ), and all other faces are triangles with a common vertex ( side faces ) (Fig. 15). The pyramid is called correct , if its base is a regular polygon and the top of the pyramid is projected into the center of the base (Fig. 16). A triangular pyramid with all edges equal is called tetrahedron .

Lateral rib of a pyramid is the side of the side face that does not belong to the base Height pyramid is the distance from its top to the base plane. All lateral edges of a regular pyramid are equal to each other, all lateral faces are equal isosceles triangles. The height of the side face of a regular pyramid drawn from the vertex is called apothem . Diagonal section is called a section of a pyramid by a plane passing through two lateral edges that do not belong to the same face.

Lateral surface area pyramid is the sum of the areas of all lateral faces. Total surface area is called the sum of the areas of all the side faces and the base.

Theorems

1. If in a pyramid all the lateral edges are equally inclined to the plane of the base, then the top of the pyramid is projected into the center of the circle circumscribed near the base.

2. If all the side edges of a pyramid have equal lengths, then the top of the pyramid is projected into the center of a circle circumscribed near the base.

3. If all the faces in a pyramid are equally inclined to the plane of the base, then the top of the pyramid is projected into the center of a circle inscribed in the base.

To calculate the volume of an arbitrary pyramid, the correct formula is:

Where V- volume;

S base– base area;

H– height of the pyramid.

For a regular pyramid, the following formulas are correct:

Where p– base perimeter;

h a– apothem;

H- height;

S full

S side

S base– base area;

V– volume of a regular pyramid.

Truncated pyramid called the part of the pyramid enclosed between the base and a cutting plane parallel to the base of the pyramid (Fig. 17). Regular truncated pyramid called the part of a regular pyramid enclosed between the base and a cutting plane parallel to the base of the pyramid.

Grounds truncated pyramid - similar polygons. Side faces – trapezoids. Height of a truncated pyramid is the distance between its bases. Diagonal a truncated pyramid is a segment connecting its vertices that do not lie on the same face. Diagonal section is a section of a truncated pyramid by a plane passing through two lateral edges that do not belong to the same face.

For a truncated pyramid the following formulas are valid:

(4)

Where S 1 , S 2 – areas of the upper and lower bases;

S full– total surface area;

S side– lateral surface area;

H- height;

V– volume of a truncated pyramid.

For a regular truncated pyramid the formula is correct:

Where p 1 , p 2 – perimeters of the bases;

h a– apothem of a regular truncated pyramid.

Example 1. In a regular triangular pyramid, the dihedral angle at the base is 60º. Find the tangent of the angle of inclination of the side edge to the plane of the base.

Solution. Let's make a drawing (Fig. 18).

The pyramid is regular, which means that at the base there is an equilateral triangle and all the side faces are equal isosceles triangles. The dihedral angle at the base is the angle of inclination of the side face of the pyramid to the plane of the base. The linear angle is the angle a between two perpendiculars: etc. The top of the pyramid is projected at the center of the triangle (the center of the circumcircle and inscribed circle of the triangle ABC). The angle of inclination of the side edge (for example S.B.) is the angle between the edge itself and its projection onto the plane of the base. For the rib S.B. this angle will be the angle SBD. To find the tangent you need to know the legs SO And O.B.. Let the length of the segment BD equals 3 A. Dot ABOUT line segment BD is divided into parts: and From we find SO: From we find:

Answer:

Example 2. Find the volume of a regular truncated quadrangular pyramid if the diagonals of its bases are equal to cm and cm, and its height is 4 cm.

Solution. To find the volume of a truncated pyramid, we use formula (4). To find the area of ​​the bases, you need to find the sides of the base squares, knowing their diagonals. The sides of the bases are equal to 2 cm and 8 cm, respectively. This means the areas of the bases and Substituting all the data into the formula, we calculate the volume of the truncated pyramid:

Answer: 112 cm 3.

Example 3. Find the area of ​​the lateral face of a regular triangular truncated pyramid, the sides of the bases of which are 10 cm and 4 cm, and the height of the pyramid is 2 cm.

Solution. Let's make a drawing (Fig. 19).

The side face of this pyramid is an isosceles trapezoid. To calculate the area of ​​a trapezoid, you need to know the base and height. The bases are given according to the condition, only the height remains unknown. We'll find her from where A 1 E perpendicular from a point A 1 on the plane of the lower base, A 1 D– perpendicular from A 1 per AC. A 1 E= 2 cm, since this is the height of the pyramid. To find DE Let's make an additional drawing showing the top view (Fig. 20). Dot ABOUT– projection of the centers of the upper and lower bases. since (see Fig. 20) and On the other hand OK– radius inscribed in the circle and OM– radius inscribed in a circle:

MK = DE.

According to the Pythagorean theorem from

Side face area:

Answer:

Example 4. At the base of the pyramid lies an isosceles trapezoid, the bases of which A And b (a> b). Each side face forms an angle equal to the plane of the base of the pyramid j. Find the total surface area of ​​the pyramid.

Solution. Let's make a drawing (Fig. 21). Total surface area of ​​the pyramid SABCD equal to the sum of the areas and the area of ​​the trapezoid ABCD.

Let us use the statement that if all the faces of the pyramid are equally inclined to the plane of the base, then the vertex is projected into the center of the circle inscribed in the base. Dot ABOUT– vertex projection S at the base of the pyramid. Triangle SOD is the orthogonal projection of the triangle CSD to the plane of the base. Using the theorem on the area of ​​the orthogonal projection of a plane figure, we obtain:

Likewise it means Thus, the problem was reduced to finding the area of ​​the trapezoid ABCD. Let's draw a trapezoid ABCD separately (Fig. 22). Dot ABOUT– the center of a circle inscribed in a trapezoid.

Since a circle can be inscribed in a trapezoid, then or From the Pythagorean theorem we have

A three-dimensional figure that often appears in geometric problems is the pyramid. The simplest of all the figures in this class is triangular. In this article we will analyze in detail the basic formulas and properties of the correct

Geometric ideas about the figure

Before moving on to considering the properties of a regular triangular pyramid, let’s take a closer look at what kind of figure we are talking about.

Let's assume that there is an arbitrary triangle in three-dimensional space. Let us select any point in this space that does not lie in the plane of the triangle and connect it with the three vertices of the triangle. We got a triangular pyramid.

It consists of 4 sides, all of which are triangles. The points where three faces meet are called vertices. The figure also has four of them. The lines of intersection of two faces are edges. The pyramid in question has 6 edges. The figure below shows an example of this figure.

Since the figure is formed by four sides, it is also called a tetrahedron.

Correct pyramid

Above we considered an arbitrary figure with a triangular base. Now suppose that we draw a perpendicular segment from the top of the pyramid to its base. This segment is called height. Obviously, you can draw 4 different heights for the figure. If the height intersects the triangular base at the geometric center, then such a pyramid is called straight.

A straight pyramid, the base of which is an equilateral triangle, is called regular. For her, all three triangles forming the lateral surface of the figure are isosceles and equal to each other. A special case of a regular pyramid is the situation when all four sides are equilateral identical triangles.

Let's consider the properties of a regular triangular pyramid and give the corresponding formulas for calculating its parameters.

Base side, height, lateral edge and apothem

Any two of the listed parameters uniquely determine the other two characteristics. Let us present formulas that relate these quantities.

Let us assume that the side of the base of a regular triangular pyramid is a. The length of its lateral edge is b. What will be the height of a regular triangular pyramid and its apothem?

For height h we get the expression:

This formula follows from the Pythagorean theorem for which the side edge, the height and 2/3 of the height of the base are.

The apothem of a pyramid is the height for any side triangle. The length of the apothem a b is equal to:

a b = √(b 2 - a 2 /4)

From these formulas it is clear that whatever the side of the base of a triangular regular pyramid and the length of its side edge, the apothem will always be greater than the height of the pyramid.

The two formulas presented contain all four linear characteristics of the figure in question. Therefore, given the known two of them, you can find the rest by solving the system of written equalities.

Figure volume

For absolutely any pyramid (including an inclined one), the value of the volume of space limited by it can be determined by knowing the height of the figure and the area of ​​its base. The corresponding formula is:

Applying this expression to the figure in question, we obtain the following formula:

Where the height of a regular triangular pyramid is h and its base side is a.

It is not difficult to obtain a formula for the volume of a tetrahedron in which all sides are equal to each other and represent equilateral triangles. In this case, the volume of the figure is determined by the formula:

That is, it is determined uniquely by the length of side a.

Surface area

Let us continue to consider the properties of a regular triangular pyramid. The total area of ​​all the faces of a figure is called its surface area. The latter can be conveniently studied by considering the corresponding development. The figure below shows what the development of a regular triangular pyramid looks like.

Let's assume that we know the height h and the side of the base a of the figure. Then the area of ​​its base will be equal to:

Every schoolchild can obtain this expression if he remembers how to find the area of ​​a triangle, and also takes into account that the altitude of an equilateral triangle is also a bisector and a median.

The lateral surface area formed by three identical isosceles triangles is:

S b = 3/2*√(a 2 /12+h 2)*a

This equality follows from the expression of the apothem of the pyramid in terms of the height and length of the base.

The total surface area of ​​the figure is:

S = S o + S b = √3/4*a 2 + 3/2*√(a 2 /12+h 2)*a

Note that for a tetrahedron in which all four sides are identical equilateral triangles, the area S will be equal to:

Properties of a regular truncated triangular pyramid

If the top of the considered triangular pyramid is cut off with a plane parallel to the base, then the remaining lower part will be called a truncated pyramid.

In the case of a triangular base, the result of the described sectioning method is a new triangle, which is also equilateral, but has a shorter side length than the side of the base. A truncated triangular pyramid is shown below.

We see that this figure is already limited by two triangular bases and three isosceles trapezoids.

Let us assume that the height of the resulting figure is equal to h, the lengths of the sides of the lower and upper bases are a 1 and a 2, respectively, and the apothem (height of the trapezoid) is equal to a b. Then the surface area of ​​the truncated pyramid can be calculated using the formula:

S = 3/2*(a 1 +a 2)*a b + √3/4*(a 1 2 + a 2 2)

Here the first term is the area of ​​the lateral surface, the second term is the area of ​​the triangular bases.

The volume of the figure is calculated as follows:

V = √3/12*h*(a 1 2 + a 2 2 + a 1 *a 2)

To unambiguously determine the characteristics of a truncated pyramid, it is necessary to know its three parameters, as demonstrated by the given formulas.

Video tutorial 2: Pyramid problem. Volume of the pyramid

Video tutorial 3: Pyramid problem. Correct pyramid

Lecture: Pyramid, its base, lateral ribs, height, lateral surface; triangular pyramid; regular pyramid

Pyramid is a three-dimensional body that has a polygon at its base, and all its faces consist of triangles.

A special case of a pyramid is a cone with a circle at its base.

Let's look at the main elements of the pyramid:

Apothem- this is a segment that connects the top of the pyramid with the middle of the lower edge of the side face. In other words, this is the height of the edge of the pyramid.

In the figure you can see triangles ADS, ABS, BCS, CDS. If you look closely at the names, you can see that each triangle has one common letter in its name - S. That is, this means that all the side faces (triangles) converge at one point, which is called the top of the pyramid.

The segment OS that connects the vertex with the point of intersection of the diagonals of the base (in the case of triangles - at the point of intersection of the heights) is called pyramid height.

A diagonal section is a plane that passes through the top of the pyramid, as well as one of the diagonals of the base.

Since the side surface of the pyramid consists of triangles, to find the total area of ​​the side surface it is necessary to find the area of ​​each face and add them up. The number and shape of faces depends on the shape and size of the sides of the polygon that lies at the base.

The only plane in a pyramid that does not belong to its vertex is called basis pyramids.

In the figure we see that the base is a parallelogram, however, it can be any arbitrary polygon.

Properties:

Consider the first case of a pyramid, in which it has edges of the same length:

• A circle can be drawn around the base of such a pyramid. If you project the top of such a pyramid, then its projection will be located in the center of the circle.
• The angles at the base of the pyramid are the same on each face.
• In this case, a sufficient condition for the fact that a circle can be described around the base of the pyramid, and also that all the edges are of different lengths, can be considered the same angles between the base and each edge of the faces.

If you come across a pyramid in which the angles between the side faces and the base are equal, then the following properties are true:

• You will be able to describe a circle around the base of the pyramid, the apex of which is projected exactly at the center.
• If you draw each side edge of the height to the base, then they will be of equal length.
• To find the lateral surface area of ​​such a pyramid, it is enough to find the perimeter of the base and multiply it by half the length of the height.
• S bp = 0.5P oc H.
• Types of pyramid.
• Depending on which polygon lies at the base of the pyramid, they can be triangular, quadrangular, etc. If at the base of the pyramid there is a regular polygon (with equal sides), then such a pyramid will be called regular.

Regular triangular pyramid